
如图,正方体ABCD—A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.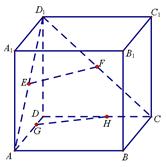
(1)求GH长的取值范围;
(2)当GH取得最小值时,求证:EH与FG共面;并求出此时EH与FG的交点P到直线 的距离.
的距离.
(1)[2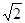 ,4] (2)
,4] (2)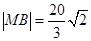
解析试题分析:解:(1)以D为原点,DA,DC,DD1分别为x轴,y轴,z轴建立空间直角坐标系.
设DG=a,DH=b,则E(4,0,4),F(0,4,4),G(a,0,0),H(0,b,0).
∴ =(-4,b,-4),
=(-4,b,-4), =(a,-4,-4).
=(a,-4,-4).
∵EH⊥FG.
∴ ·
· =-4a-4b+16=0,则a+b=4,即b=4-a.
=-4a-4b+16=0,则a+b=4,即b=4-a.
又G1H在棱DA,DC上,则0≤a≤8,0≤b≤8,从而0≤a≤4.
∴GH=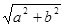 =
=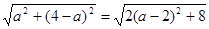 .
.
∴GH取值范围是[2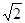 ,4] . ……6分
,4] . ……6分
(2)当GH=2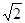 时,a=2,b=2.
时,a=2,b=2.
∴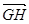 =(-2,2,0),
=(-2,2,0),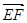 =(-4,4,0),即
=(-4,4,0),即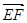 =2
=2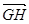 .
.
∴EF∥GH,即EH与FG共面.
所以EF=2GH,EF∥GH,则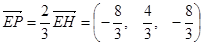 .
.
设P(x1,y1,z1),则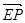 =(x1-4,y,z1-4).
=(x1-4,y,z1-4).
∴x1=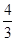 ,y1=
,y1=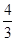 ,z1=
,z1=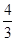 ,即P(
,即P(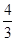 ,
,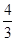 ,
,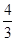 ).
).
则P(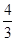 ,
,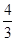 ,
,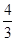 )在底面上ABCD上的射影为M(
)在底面上ABCD上的射影为M(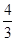 ,
,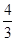 ,0).又B(8,8,0),
,0).又B(8,8,0),
所以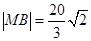 为点P到直线
为点P到直线 的距离. ……12分
的距离. ……12分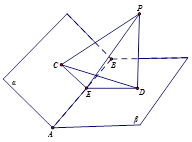
考点:空间中两点的距离,点到直线的距离
点评:关键是通过建立空间直角坐标系,然后表示点的坐标以及点在平面的射影得到距离,属于基础题。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=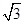 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.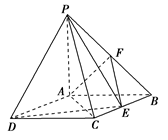
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)求证:无论点E在BC边的何处,都有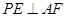 ;
;
(3)当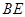 为何值时,
为何值时,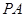 与平面
与平面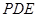 所成角的大小为45°.
所成角的大小为45°.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,将边长为2的正方形ABCD沿对角线BD折叠,使的平面ABD⊥平面CBD,AE⊥平面ABD,且AE=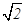 ,
,
(1) 求证:DE⊥AC
(2)求DE与平面BEC所成角的正弦值
(3)直线BE上是否存在一点M,使得CM//平面ADE,若存在,求M的位置,不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,S是正方形ABCD所在平面外一点,且SD⊥面ABCD ,AB=1,SB=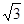 .
.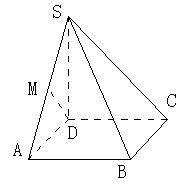
(1)求证:BC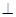 SC;
SC;
(2) 设M为棱SA中点,求异面直线DM与SB所成角的大小
(3) 求面ASD与面BSC所成二面角的大小;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面是直角梯形,AB⊥AD,点E在线段AD上,且CE∥AB。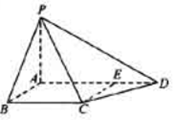
求证:CE⊥平面PAD;
(11)若PA=AB=1,AD=3,CD=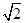 ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四边形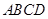 中,
中, 为正三角形,
为正三角形, ,
,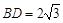 ,
, 与
与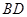 交于
交于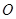 点.将
点.将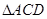 沿边
沿边 折起,使
折起,使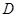 点至
点至 点,已知
点,已知 与平面
与平面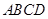 所成的角为
所成的角为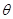 ,且
,且 点在平面
点在平面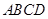 内的射影落在
内的射影落在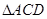 内.
内.
(Ⅰ)求证: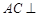 平面
平面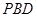 ;
;
(Ⅱ)若已知二面角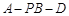 的余弦值为
的余弦值为 ,求
,求 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥 中,
中, 底面
底面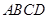 ,
,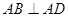 ,
,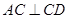 ,
,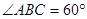 ,
,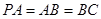 .
.
(1)若E是PC的中点,证明: 平面
平面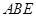 ;
;
(2)试在线段PC上确定一点E,使二面角P- AB- E的大小为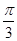 ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点,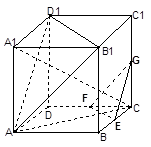
(1)求证:平面A B1D1∥平面EFG;
(2)求证:平面AA1C⊥面EFG.
(3)求异面直线AC与A1B所成的角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com