
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 在
在![]() 上的单调区间;
上的单调区间;
(3)求![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(1)a=2,b=-4;(2)![]() 的增区间为
的增区间为 ![]() ;减区间为
;减区间为![]() ;(3)13.
;(3)13.
【解析】
(1)先对f(x)求导,把x=1代入导数式即可解出曲线在![]() 处的斜率k;把x=1代入原函数即可解出切点纵坐标,建立一个关于a和b的二元一次方程组,解方程可得a,b的值;
处的斜率k;把x=1代入原函数即可解出切点纵坐标,建立一个关于a和b的二元一次方程组,解方程可得a,b的值;
(2)求出f(x)的导数,由导数大于0,可得增区间;导数小于0,可得减区间;
(3)分别求出f(x)在区间[﹣3,1]上的极值和区间端点处的函数值,比较大小找出最大的值,即为函数在该闭区间上的最大值。
(1) 函数 ![]() 的导数为
的导数为 ![]() ,
,
曲线 ![]() 在点
在点 ![]() 处的切线斜率为
处的切线斜率为![]() ,
,
切点为![]() ,
,
由切线方程为 ![]() ,可得
,可得 ![]() ,
,![]() ,
,
解得![]() .
.
(2) 函数 ![]() 的导数
的导数![]() ,由
,由 ![]() ,可得
,可得 ![]() 或
或 ![]() ;由
;由 ![]() ,可得
,可得 ![]() .则 f(x) 的增区间为
.则 f(x) 的增区间为 ![]() ,
,![]() ;减区间为
;减区间为 ![]() .
.
(3) 由(2)可得 f(x) 的两极值点-2,![]() ,
,
![]() ,
,![]() ,
,
又 ![]() ,
,![]() .
.
故 y=f(x) 在 ![]() 上的最大值为 13.
上的最大值为 13.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了![]() 名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于
名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于![]() 分钟的观众称为体育迷.
分钟的观众称为体育迷.
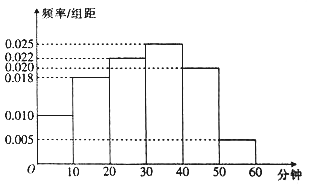
(1)以频率为概率,若从这![]() 名观众中随机抽取
名观众中随机抽取![]() 名进行调查,求这
名进行调查,求这![]() 名观众中体育迷人数
名观众中体育迷人数![]() 的分布列;
的分布列;
(2)若抽取![]() 人中有女性
人中有女性![]() 人,其中女体育迷有
人,其中女体育迷有![]() 人,完成答题卡中的列联表并判断能否在犯错概率不超过
人,完成答题卡中的列联表并判断能否在犯错概率不超过![]() 的前提下认为是体育迷与性别有关系吗?
的前提下认为是体育迷与性别有关系吗?
附表及公式:
|
|
|
|
|
|
|
|
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据.
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)试根据(1)求出的线性回归方程,预测燃放烟花爆竹的天数为9的雾霾天数.
相关公式: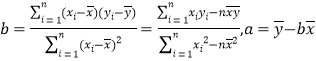
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x2的图象在点(x0 , x02)处的切线为l,若l也与函数y=lnx,x∈(0,1)的图象相切,则x0必满足( )
A.0<x0< ![]()
B.![]() <x0<1
<x0<1
C.![]() <x0<
<x0< ![]()
D.![]() <x0
<x0 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=logax(a>1)在[a,2a]上的最大值是最小值的2倍.
(1)若函数g(x)=f(3x2-mx+5)在区间[-1,+∞)上是增函数,求实数m的取值范围;
(2)设函数F(x)=f(![]() )(2x),且关于x的方程F(x)=k在[
)(2x),且关于x的方程F(x)=k在[![]() ,4]上有解,求实数k的取值范围.
,4]上有解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且经过点
,且经过点![]() ,直线
,直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() .
.
(1)求椭圆的方程;
(2)求![]() 的取值范围;
的取值范围;
(3)若直线![]() 不过点
不过点![]() ,求证:直线
,求证:直线![]() 的斜率互为相反数.
的斜率互为相反数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点. (Ⅰ)证明:A1O⊥平面ABC;
(Ⅱ)求二面角A﹣A1B﹣C1的大小.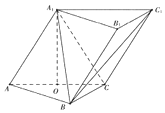
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的方程(x﹣1)4+mx﹣m﹣2=0各个实根x1 , x2…xk(k≤4,k∈N*)所对应的点(xi![]() ),(i=1,2,3…k)均在直线y=x的同侧,则实数m的取值范围是( )
),(i=1,2,3…k)均在直线y=x的同侧,则实数m的取值范围是( )
A.(﹣1,7)
B.(﹣∞,﹣7)U(﹣1,+∞)
C.(﹣7,1)
D.(﹣∞,1)U(7,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com