解:(Ⅰ)设该等差数列为{a
n},
则a
1=a,a
2=4,a
3=3a,S
k=2550.
由已知有a+3a=2×4,
解得首项a
1=a=2,
公差d=a
2-a
1=2.
代入公式S
k=k•a
1+
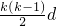
得
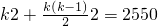
∴k
2+k-2550=0
解得k=50,k=-51(舍去)
∴a=2,k=50;
(Ⅱ)由
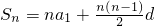
得S
n=n(n+1),
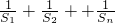
=
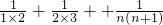
=
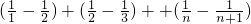
=

∴
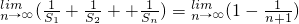
=1.
分析:(Ⅰ)设该等差数列为{a
n},由题设条件可知首项a
1=2,公差d=2.由此可以求得a=2,k=50.
(Ⅱ)由
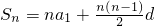
,得S
n=n(n+1),
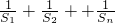
=

,由此求得求
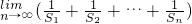
的值.
点评:本题考查数列的极限,解题时要认真审题,仔细解答,避免不必要的错误.

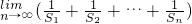 .
.