
【题目】已知数列![]() 满足:
满足:![]() ,
,![]() ,且
,且![]() (n=1,2,...).记
(n=1,2,...).记
集合![]() .
.
(1)(Ⅰ)若![]() ,写出集合M的所有元素;
,写出集合M的所有元素;
(2)(Ⅱ)若集合M存在一个元素是3的倍数,证明:M的所有元素都是3的倍数;
(3)(Ⅲ)求集合M的元素个数的最大值.
【答案】
(1)
{6,12,24}
(2)
证明:(Ⅱ)因为集合M存在一个元素是3的倍数,所以不妨设 ak 是3的倍数,由已知 ![]() ,可用用数学归纳法证明对任意 n ≥ k , an 是3的倍数,当 k = 1 时,则M中的所有元素都是3的倍数,如果 k > 1 时,因为 ak = 2ak-1 或 2ak-1 -36 ,所以 2ak-1 是3的倍数,于是 ak-1 是3的倍数,类似可得, ak -2 . . . . . . a1 都是3的倍数,从而对任意 n ≥ 1 , an 是3的倍数,因此M的所有元素都是3的倍数.
,可用用数学归纳法证明对任意 n ≥ k , an 是3的倍数,当 k = 1 时,则M中的所有元素都是3的倍数,如果 k > 1 时,因为 ak = 2ak-1 或 2ak-1 -36 ,所以 2ak-1 是3的倍数,于是 ak-1 是3的倍数,类似可得, ak -2 . . . . . . a1 都是3的倍数,从而对任意 n ≥ 1 , an 是3的倍数,因此M的所有元素都是3的倍数.
(3)
8
【解析】(Ⅰ)由已知![]() 可知:
可知:![]() ,因此
,因此![]() 。
。
(Ⅱ)因为集合M存在一个元素是3的倍数,所以不妨设![]() 是3的倍数,由已知
是3的倍数,由已知![]() ,可用用数学归纳法证明对任意
,可用用数学归纳法证明对任意![]() ,
,![]() 是3的倍数,当
是3的倍数,当![]() 时,则M中的所有元素都是3的倍数,如果
时,则M中的所有元素都是3的倍数,如果![]() 时,因为
时,因为![]() 或
或![]() ,所以
,所以![]() 是3的倍数,于是
是3的倍数,于是![]() 是3的倍数,类似可得,
是3的倍数,类似可得,![]() 都是3的倍数,从而对任意
都是3的倍数,从而对任意![]() ,
,![]() 是3的倍数,因此M的所有元素都是3的倍数.
是3的倍数,因此M的所有元素都是3的倍数.
(III )由于M中的元素都不超过36,由![]() ,易得
,易得![]() ,类似可得
,类似可得![]() ,其次M中的元素个数最多除了前面两个数外,都是4的倍数,因为第二哥数必定为偶数,由
,其次M中的元素个数最多除了前面两个数外,都是4的倍数,因为第二哥数必定为偶数,由![]() 的定义可知,第三个数后面的数必定是4的倍数,另外,M中的数除以9的余数,由定义可知,
的定义可知,第三个数后面的数必定是4的倍数,另外,M中的数除以9的余数,由定义可知,![]() 和
和![]() 除以9的余数一样,
除以9的余数一样,
(1)若![]() 中有3的倍数,由(2)知:所有
中有3的倍数,由(2)知:所有![]() 都是3的倍数,所以
都是3的倍数,所以![]() 都是3的倍数,所以
都是3的倍数,所以![]() 除以9的余数为3,6,3,6,......,或6,3,6,3......,或0,0,0......,而除以9余3且是4的倍数只有12,除以9余6且是4的倍数只有24,除以9余0且是4的倍数只有36,则M中的数从第三项起最多2项,加上前面两项,最多4项。
除以9的余数为3,6,3,6,......,或6,3,6,3......,或0,0,0......,而除以9余3且是4的倍数只有12,除以9余6且是4的倍数只有24,除以9余0且是4的倍数只有36,则M中的数从第三项起最多2项,加上前面两项,最多4项。
(2)若![]() 中没有3的倍数,则
中没有3的倍数,则![]() 都不是3的倍数,对于
都不是3的倍数,对于![]() 除以9的余数只能是1,4,7,2,5,8中的一个,从
除以9的余数只能是1,4,7,2,5,8中的一个,从![]() 起,
起,![]() 除以9的余数是1,2,4,8,7,5,1,2,4,8,......,不断的6项循环(可能从2,4,8,7或5开始),而除以9的余数是1,2,4,8,5且是4的倍数(不大于36),只有28,20,4,8,16,32,所以M中的项加上前两项最多的8项,则
除以9的余数是1,2,4,8,7,5,1,2,4,8,......,不断的6项循环(可能从2,4,8,7或5开始),而除以9的余数是1,2,4,8,5且是4的倍数(不大于36),只有28,20,4,8,16,32,所以M中的项加上前两项最多的8项,则![]() 时,
时,![]() ,项数为8,所以集合M的元素个数的最大值为8.
,项数为8,所以集合M的元素个数的最大值为8.
【考点精析】根据题目的已知条件,利用数学归纳法的步骤的相关知识可以得到问题的答案,需要掌握
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 ![]() (t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位.且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=6sinθ.
(t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位.且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=6sinθ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B.若点P的坐标为(1,2),求|PA|+|PB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱![]() 的底面是正三角形,侧面
的底面是正三角形,侧面![]() 为菱形,且
为菱形,且![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
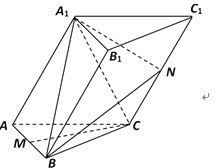
(I)求证:![]() ∥平面
∥平面![]() ;
;
(II)求证:![]() ;
;
(III)求BA1与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线 ![]() :
: ![]() ,点
,点 ![]() 的极坐标为
的极坐标为 ![]() ,直线
,直线 ![]() 的极坐标方程为
的极坐标方程为 ![]() ,且点
,且点 ![]() 在直线
在直线 ![]() 上.
上.
(1)求曲线 ![]() 的极坐标方程和直线
的极坐标方程和直线 ![]() 的直角坐标方程;
的直角坐标方程;
(2)设 ![]() 向左平移
向左平移 ![]() 个单位长度后得到
个单位长度后得到 ![]() ,
, ![]() 到
到 ![]() 的交点为
的交点为 ![]() ,
, ![]() ,求
,求 ![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛两次,记第一次出现的点数为 ![]() ,第二次出现的点数为
,第二次出现的点数为 ![]() ,则事件“
,则事件“ ![]() ”的概率为( )
”的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是由正整数构成的数表,用aij表示i行第j个数(i,j∈N+).此表中ail=aii=i,每行中除首尾两数外,其他各数分别等于其“肩膀”上的两数之和.

(1)写出数表的第六行(从左至右依次列出).
(2)设第n行的第二个数为bn(n≥2),求bn.
(3)令![]() ,记Tn为数列
,记Tn为数列![]() 前n项和,求
前n项和,求![]() 的最大值,并求此时n的值.
的最大值,并求此时n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】E为正四面体D﹣ABC棱AD的中点,平面α过点A,且α∥平面ECB,α∩平面ABC=m,α∩平面ACD=n,则m、n所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com