
已知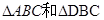 所在的平面互相垂直,且AB=BC=BD,
所在的平面互相垂直,且AB=BC=BD,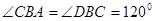 ,求:
,求:
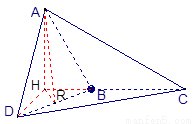
⑴.直线AD与平面BCD所成角的大小;
⑵.直线AD与直线BC所成角的大小;
⑶.二面角A-BD-C的余弦值.
⑴∠ADH=45°⑵90°⑶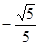
【解析】(1)本小题关键是找出线面角,在平面ABC内,过A作AH⊥BC,垂足为H,
则AH⊥平面DBC,∴∠ADH即为直线AD与平面BCD所成的角.
(2)易证 ,所以
,所以 ,所以直线AD与直线BC所成角为
,所以直线AD与直线BC所成角为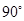 .
.
(3)找(做)出二面角A-BD-C的平面角是解决本小题的关键.本小题可采用三垂线定理定角法.过H作HR⊥BD,垂足为R,连结AR,则由三垂线定理知,AR⊥BD,故∠ARH 为二面角A—BD—C的平面角的补角.
为二面角A—BD—C的平面角的补角.
解:⑴如图,在平面ABC内,过A作AH⊥BC,垂足为H,
则AH⊥平面DBC,∴∠ADH即为直线AD与平面BCD所成的角
由题设知△AHB≌△AHD,则DH⊥BH,AH=DH,∴∠ADH=45°…………….5分
⑵∵BC⊥DH,且DH为AD在平面BCD上的射影, ∴BC⊥AD,
故AD与BC所成的角为90° ……9分
⑶过H作HR⊥BD,垂足为R,连结AR,则由三垂线定理知,AR⊥BD,故∠ARH 为二面角A—BD—C的平面角的补角 设BC=a,则由题设知,AH=DH=
为二面角A—BD—C的平面角的补角 设BC=a,则由题设知,AH=DH=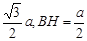 ,在△HDB中,HR=
,在△HDB中,HR=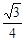 a,∴tanARH=
a,∴tanARH=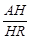 =2
=2
故二面角A—BD—C的余弦值的大小为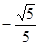 …………14分
…………14分


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源:2011-2012学年辽宁省沈阳四校高三上学期12月月考理科数学试卷 题型:解答题
已知如图几何体,正方形 和矩形
和矩形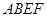 所在平面互相垂
所在平面互相垂
直,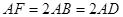 ,
,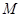 为
为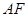 的中点,
的中点,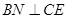 。
。
(Ⅰ)求证: 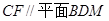 ;
;
(Ⅱ)求二面角 的大小。
的大小。

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| OH |
查看答案和解析>>
科目:高中数学 来源:2010年新教材高考数学模拟题详解精编试卷(4)(解析版) 题型:解答题
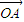 =
=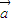 ,
,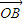 =
=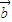 ,
,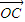 =
=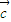 ,OA,OB,OC两两互相垂直,H为△ABC的垂心,试用
,OA,OB,OC两两互相垂直,H为△ABC的垂心,试用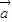 ,
,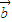 ,
,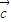 表示
表示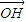 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com