
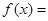
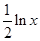
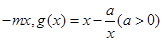 .
.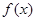 的单调区间;
的单调区间;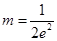 ,对
,对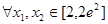 都有
都有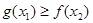 成立,求实数
成立,求实数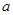 的取值范围;
的取值范围;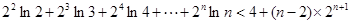 (
(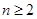 且
且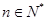 ).
). 时,
时,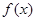 单调递增区间为(0,+∞).当m>0时,
单调递增区间为(0,+∞).当m>0时,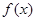 单调递增区间为(0,
单调递增区间为(0,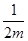 ),单调递减区间为(
),单调递减区间为(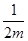 ,+∞). (Ⅱ)实数
,+∞). (Ⅱ)实数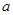 的取值范围为
的取值范围为 .(Ⅲ)详见解析.
.(Ⅲ)详见解析.

 都有
都有 ”,
”,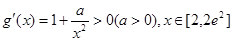 ,得到函数
,得到函数 在[2,2
在[2,2 ]上是增函数,
]上是增函数, =g(2)=2-
=g(2)=2- ,利用2-
,利用2-

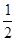 ,及
,及 得到实数
得到实数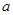 的取值范围为
的取值范围为 .
. ,利用(I)确定
,利用(I)确定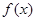 的单调性得到
的单调性得到 ,(当
,(当 时取“=”号),利用“错位相减法”求得S=
时取“=”号),利用“错位相减法”求得S=
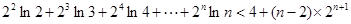 (
( ).
).
 1分
1分 时
时 ,
,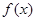 在(0,+∞)单调递增. 2分
在(0,+∞)单调递增. 2分 得
得
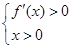 得
得
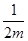
 得
得 >
>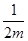 4分
4分 时,
时,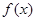 单调递增区间为(0,+∞).
单调递增区间为(0,+∞).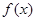 单调递增区间为(0,
单调递增区间为(0,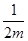 ),单调递减区间为(
),单调递减区间为(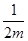 ,+∞). 5分
,+∞). 5分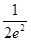 ,
, ,对
,对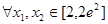 都有
都有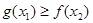 成立等价于对
成立等价于对

 都有
都有 6分
6分 ]上
]上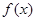 的最大值
的最大值 =
=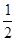 7分
7分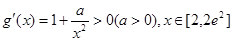
 在[2,2
在[2,2 ]上是增函数,
]上是增函数, =g(2)=2-
=g(2)=2- , 9分
, 9分

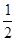 ,得
,得 ,又因为
,又因为 ,∴
,∴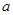 ∈
∈
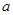 的取值范围为
的取值范围为 . 10分
. 10分 令m=
令m=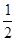 ,则
,则
 ,(当x=1时取“=”号)
,(当x=1时取“=”号)
 11分
11分

 12分
12分 ①
① ②
②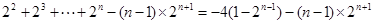
 S=
S=

 (
( ) 14分
) 14分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com