
【题目】如图,四棱锥![]() 的底面
的底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)当四棱锥![]() 的体积最大时,求平面
的体积最大时,求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:⑴由条件推出四边形![]() 是矩形,得到
是矩形,得到![]() ,再推出
,再推出![]() ,
, ![]() 平面
平面![]() ,即可推出平面
,即可推出平面![]() 平面
平面![]()
⑵要使四棱锥![]() 的体积取最大值,只需
的体积取最大值,只需![]() 取得最大值,当且仅当
取得最大值,当且仅当![]() 时,
时, ![]() 取得最大值36,分别以
取得最大值36,分别以![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,利用向量法求出平面
,利用向量法求出平面![]() 与平面
与平面![]() 所成角的余弦值
所成角的余弦值
解析:(1)由![]() 可得
可得![]() ,
,
易得四边形![]() 是矩形,∴
是矩形,∴![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]()
(2)四棱锥![]() 的体积为
的体积为![]() ,
,
要使四棱锥![]() 的体积取最大值,只需
的体积取最大值,只需![]() 取得最大值.
取得最大值.
由条件可得![]() ,
,
∴![]() ,即
,即![]() ,
,
当且仅当![]() 时,
时, ![]() 取得最大值36.
取得最大值36.
分别以![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .
.

则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由![]() ,
, ![]() 可得
可得
![]() ,令
,令![]() 可得
可得![]() ,
,
同理可得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 与平面
与平面![]() 所成二面角为
所成二面角为![]() ,
,
 .
.
由于平面![]() 与平面
与平面![]() 所成角为锐二面角,所以余弦值为
所成角为锐二面角,所以余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在某单位的食堂中,食堂每天以10元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂购进了80斤米粉,以![]() (斤)(其中
(斤)(其中![]() )表示米粉的需求量,
)表示米粉的需求量, ![]() (元)表示利润.
(元)表示利润.
(1)估计该天食堂利润不少于760元的概率;
(2)在直方图的需求量分组中,以区间中间值作为该区间的需求量,以需求量落入该区间的频率作为需求量在该区间的概率,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中点在原点,焦点在
的中点在原点,焦点在![]() 轴上,离心率
轴上,离心率![]() ,以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为
,以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点![]() 的两条直线
的两条直线![]() ,
, ![]() ,交椭圆
,交椭圆![]() 于
于![]() ,
, ![]() ,
, ![]() ,
, ![]() 四点,若
四点,若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点的横坐标都缩短为原来的
上各点的横坐标都缩短为原来的![]() 倍,纵坐标坐标都伸长为原来的
倍,纵坐标坐标都伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,在极坐标系(与直角坐标系
,在极坐标系(与直角坐标系![]() 取相同的单位长度,且以原点
取相同的单位长度,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市县乡教师流失现象非常严重,为了县乡孩子们能接受良好教育,某市今年要为两所县乡中学招聘储备未来三年的教师,现在每招聘一名教师需要1万元,若三年后教师严重短缺时再招聘,由于各种因素,则每招聘一名教师需要3万元,已知现在该市县乡中学无多余教师,为决策应招聘多少县乡教师搜集并整理了该市50所县乡中学在过去三年内的教师流失数,得到如表的频率分布表:
流失教师数 | 6 | 7 | 8 | 9 |
频数 | 10 | 15 | 15 | 10 |
以这50所县乡中学流失教师数的频率代替一所县乡中学流失教师数发生的概率,记![]() 表示两所县乡中学在过去三年共流失的教师数,
表示两所县乡中学在过去三年共流失的教师数, ![]() 表示今年为两所县乡中学招聘的教师数.为保障县乡孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘.
表示今年为两所县乡中学招聘的教师数.为保障县乡孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘.
(1)求![]() 的分布列;
的分布列;
(2)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(3)以未来四年内招聘教师所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 设随机变量![]() ,则
,则![]()
B. 线性回归直线不一定过样本中心点![]()
C. 若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于1
的值越接近于1
D. 先把高三年级的2000名学生编号:1到2000,再从编号为1到50的50名学生中随机抽取1名学生,其编号为![]() ,然后抽取编号为
,然后抽取编号为![]() ,
, ![]() ,
, ![]() ,……的学生,这样的抽样方法是分层抽样
,……的学生,这样的抽样方法是分层抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知鸡的产蛋量与鸡舍的温度有关,为了确定下一个时段鸡舍的控制温度,某企业需要了解鸡舍的温度![]() (单位:
(单位:![]() ),对某种鸡的时段产蛋量
),对某种鸡的时段产蛋量![]() (单位:
(单位:![]() ) 和时段投入成本
) 和时段投入成本![]() (单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度
(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度![]() 和产蛋量
和产蛋量![]() 的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
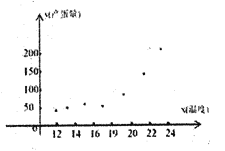
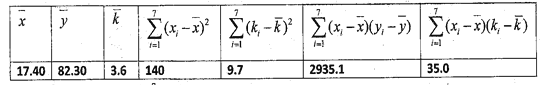
其中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作为该种鸡的时段产蛋量
哪一个更适宜作为该种鸡的时段产蛋量![]() 关于鸡舍时段控制温度
关于鸡舍时段控制温度![]() 的回归方程类型?(给判断即可,不必说明理由)
的回归方程类型?(给判断即可,不必说明理由)
(2)若用![]() 作为回归方程模型,根据表中数据,建立
作为回归方程模型,根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知时段投入成本![]() 与
与![]() 的关系为
的关系为![]() ,当时段控制温度为
,当时段控制温度为![]() 时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
附:①对于一组具有线性相关关系的数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为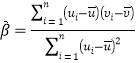 ,
,![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间几何体![]() 中,
中, ![]() 与
与![]() 均为边长为
均为边长为![]() 的等边三角形,
的等边三角形, ![]() 为腰长为
为腰长为![]() 的等腰三角形,平面
的等腰三角形,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
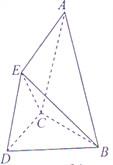
(Ⅰ)试在平面![]() 内作一条直线,使得直线上任意一点
内作一条直线,使得直线上任意一点![]() 与
与![]() 的连线
的连线![]() 均与平面
均与平面![]() 平行,并给出详细证明;
平行,并给出详细证明;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随即抽取![]() 人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的
人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的性别以及意见进行了分类,得到的数据如下表所示:
人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)根据表中的数据,能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品增多对生活无益的人员中随机抽取![]() 人,再从
人,再从![]() 人中随机抽取
人中随机抽取![]() 人赠送超市购物券作为答谢,求恰有
人赠送超市购物券作为答谢,求恰有![]() 人是女性的概率.
人是女性的概率.
参与公式: 
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com