
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,短轴的两个端点分别为A,B,且满足:
,短轴的两个端点分别为A,B,且满足:![]() ,且椭圆经过点
,且椭圆经过点![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点M![]() 的动直线
的动直线![]() (与X轴不重合)与椭圆C相交于P,Q两点,在X轴上是否存在一定点T,无论直线
(与X轴不重合)与椭圆C相交于P,Q两点,在X轴上是否存在一定点T,无论直线![]() 如何转动,点T始终在以PQ为直径的圆上?若有,求点T的坐标,若无,说明理由。
如何转动,点T始终在以PQ为直径的圆上?若有,求点T的坐标,若无,说明理由。
【答案】(1)![]() ;(2)(2,0)
;(2)(2,0)
【解析】
(1)由![]() 可知,
可知,![]() ,根据椭圆过点
,根据椭圆过点![]() ,即可求出
,即可求出![]() ,由此得到椭圆的标准方程;
,由此得到椭圆的标准方程;
(2)分别讨论直线斜率存在与不存在两种情况,当斜率不存在时,联立直线与椭圆方程,解出![]() 、
、![]() 两点坐标,利用向量垂直的条件可得点
两点坐标,利用向量垂直的条件可得点![]() ,当斜率存在时,设出直线的点斜式,与椭圆联立方程,得到关于
,当斜率存在时,设出直线的点斜式,与椭圆联立方程,得到关于![]() 的一元二次方程,写出根与系数的关系,代入
的一元二次方程,写出根与系数的关系,代入![]() 中进行化简,即可得到答案。
中进行化简,即可得到答案。
(1)由![]() 可知,
可知,![]() ,又椭圆经过点
,又椭圆经过点![]() ,则
,则![]() ,由于在椭圆中
,由于在椭圆中![]() ,所以
,所以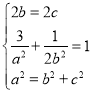 , 解得
, 解得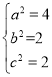 =2,所求椭圆方程为
=2,所求椭圆方程为![]()
(2) 设![]() ,
,![]() ,则
,则![]() ,
,![]()
①当直线![]() 斜率不存在时,则直线
斜率不存在时,则直线![]() 的方程为:
的方程为:![]() ,
,
联立方程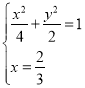 ,解得:
,解得: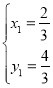 或
或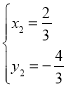 ,故点
,故点![]() ,
,![]() ;
;
则![]() ,
,![]()
由于点![]() 始终在以
始终在以![]() 为直径的圆上,则
为直径的圆上,则![]() ,解得:
,解得:![]() 或
或![]() ,故点
,故点![]() 或
或![]() ;
;
②当直线![]() 斜率
斜率![]() 存在时,设直线
存在时,设直线![]() 的方程为:
的方程为:![]() ,代入椭圆方程
,代入椭圆方程![]() 中消去
中消去![]() 得
得![]() ,
,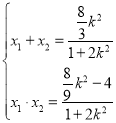
![]()
由于点![]() 始终在以
始终在以![]() 为直径的圆上,
为直径的圆上,
![]()
![]()
![]() ,
,
![]()
 解得:
解得:![]() ,故点
,故点![]() 为
为![]()
综上所述;当![]() 时满足条件。所以定点
时满足条件。所以定点![]() 为
为![]() 。
。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知![]()
![]() .
.
(1)当函数![]() 在
在![]() 上的最大值为3时,求
上的最大值为3时,求![]() 的值;
的值;
(2)在(1)的条件下,若对任意的![]() ,函数
,函数![]() ,
, ![]() 的图像与直线
的图像与直线![]() 有且仅有两个不同的交点,试确定
有且仅有两个不同的交点,试确定![]() 的值.并求函数
的值.并求函数![]() 在
在![]() 上的单调递减区间.
上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.

(1)证明:MN∥平面C1DE;
(2)求AM与平面A1MD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足![]() ,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上方程f(x)-mx-m=0有两个不同的实根,则实数m的取值范围是()
,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上方程f(x)-mx-m=0有两个不同的实根,则实数m的取值范围是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)分别求出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 在曲线
在曲线![]() 上,且
上,且![]() 到直线
到直线![]() 的距离为1,求满足这样条件的点
的距离为1,求满足这样条件的点![]() 的个数.
的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com