
动点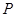 到两定点
到两定点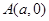 ,
,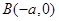 连线的斜率的乘积为
连线的斜率的乘积为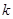 (
(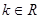 ),则动点P在以下哪些曲线上( )(写出所有可能的序号)
),则动点P在以下哪些曲线上( )(写出所有可能的序号)
① 直线 ② 椭圆 ③ 双曲线 ④ 抛物线 ⑤ 圆
A.①⑤ B.③④⑤ C.①②③⑤ D.①②③④⑤
C
【解析】
试题分析:由题设知直线PA与PB的斜率存在且均不为零
所以kPA?kPB= ,
,
整理得,点P的轨迹方程为kx2-y2=ka2(x≠±a);
① 当k>0,点P的轨迹是焦点在x轴上的双曲线(除去A,B两点)
② 当k=0,点P的轨迹是x轴(除去A,B两点)
③ 当-1<k<0时,点P的轨迹是焦点在x轴上的椭圆(除去A,B两点)
④当k=-1时,点P的轨迹是圆(除去A,B两点)
⑤当k<-1时,点P的轨迹是焦点在y轴上的椭圆(除去A,B两点).故选C.
考点:圆锥曲线的轨迹问题.
点评:本题考查圆锥曲线的轨迹问题,解题时要认真审题,注意分类讨论思想的合理运用.


科目:高中数学 来源: 题型:
| A、①⑤ | B、③④⑤ | C、①②③⑤ | D、①②③④⑤ |
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二上学期期末考试理科数学 题型:选择题
.动点 到两定点
到两定点 ,
, 连线的斜率的乘积为
连线的斜率的乘积为 (
( ),则动点P在以下哪些曲线上( )(写出所有可能的序号)
),则动点P在以下哪些曲线上( )(写出所有可能的序号)
① 直线 ② 椭圆 ③ 双曲线 ④ 抛物线 ⑤ 圆
A.①⑤ B.③④⑤ C.①②③⑤ D.①②③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com