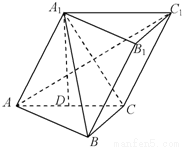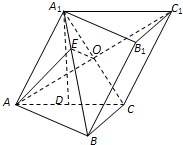
解法一--几何法:
(I)∠BCA=90°得BC⊥AC,因为A
1D⊥底ABC,所以A
1D⊥BC,A
1D∩AC=D,所以BC⊥面A
1AC,所以BC⊥AC
1因为BA
1⊥AC
1,BA
1∩BC=B,所以AC
1⊥底A
1BC
(II)由(I)得AC
1⊥A
1C,所以A
1ACC
1是菱形,
所以AC=AA
1=A
1C=2,

,
由

,得

(III)设AC
1∩A
1C=O,作OE⊥A
1B于E,连AE,由(1)所以A
1B⊥AE,所以∠AEO为二面角平面角,
在Rt△A
1BC中
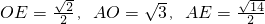
,所以
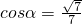
,所以二面角余弦
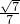
解法二--向量法:
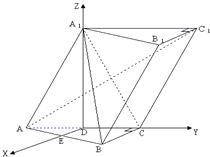
(I)如图,取AB的中点E,则DE∥BC,因为BC⊥AC,所以DE⊥AC,又A
1D⊥平面ABC,以DE,DC,DA
1为x,y,z轴建立空间坐标系,则A(0,-1,0),C(0,1,0),B(2,1,0),A
1(0,0,t),C
1(0,2,t),
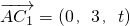
,

,
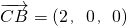
,
由
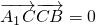
,知A
1C⊥CB,
又BA
1⊥AC
1,从而AC
1⊥平面A
1BC;
(II)由

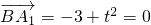
,得
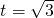
设平面A
1AB的法向量为

,
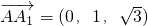
,

,所以
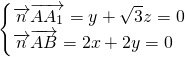
,设z=1,则
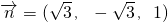
所以点C到平面A
1AB的距离
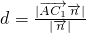
=
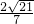
(III)再设平面A
1BC的法向量为

,
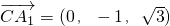
,
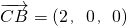
,
所以
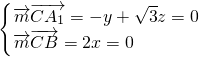
,设z=1,则
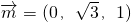
,
故
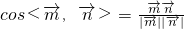
=
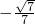
,根据法向量的方向可知二面角A-A
1B-C的余弦值大小为
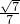
分析:解法一--几何法:
(I)根据已知中∠BCA=90°得BC⊥AC,由A
1在底面ABC上的射影恰为AC的中点D,可得A
1D⊥BC,结合线面垂直判定定理得BC⊥面A
1AC,所以BC⊥AC
1,又由BA
1⊥AC
1,再由线面垂直的判定定理,可得AC
1⊥平面A
1BC;
(Ⅱ)根据(I)的结论可得A
1ACC
1是菱形,进而根据AC=BC=2,我们可以根据

,得到点C到平面A
1AB的距离;
(Ⅲ)令AC
1∩A
1C=O,作OE⊥A
1B于E,连AE,由(I)中结论可得A
1B⊥AE,故∠AEO为二面角平面角,解三角形AEO即可得到答案.
解法二--向量法:(I)取AB的中点E,则DE∥BC,因为BC⊥AC,所以DE⊥AC,又A
1D⊥平面ABC,以DE,DC,DA
1为x,y,z轴建立空间坐标系,求出各点坐标,进而得到相应向量的坐标,利用向量垂直数量积为0,可以判断出AC
1与平面A
1BC内两条件相交直线都垂直,进而得AC
1⊥平面A
1BC;
(II)C到平面A
1AB的距离
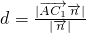
,其中

平面A
1AB的法向量,求出法向量的坐标,代入即可求出答案.
(III)分别求出平面AA
1B与平面A
1BC的法向量,代入向量夹角公式,即可求出答案.
点评:本题考查的知识点是直线与平面垂直的判定,点面之间距离的计算,二面角的平面角,解答立体几何有几何法和向量法两种方法,前者要求熟练掌握相应的判定定理、性质定理,要求有较强的逻辑性,后者可将空间问题转化为向量问题,需要记忆大量公式和较强的计算能力.

 己知三棱柱ABC-A1B1C1,A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,又知BA1⊥AC1
己知三棱柱ABC-A1B1C1,A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,又知BA1⊥AC1 解法一--几何法:
解法一--几何法: ,
, ,得
,得
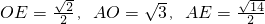 ,所以
,所以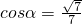 ,所以二面角余弦
,所以二面角余弦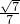

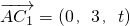 ,
, ,
,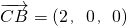 ,
,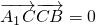 ,知A1C⊥CB,
,知A1C⊥CB,
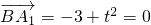 ,得
,得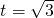
 ,
,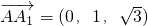 ,
, ,所以
,所以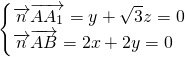 ,设z=1,则
,设z=1,则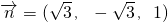
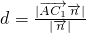 =
=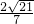
 ,
,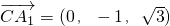 ,
,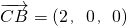 ,
,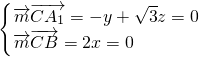 ,设z=1,则
,设z=1,则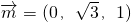 ,
,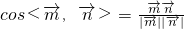 =
=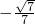 ,根据法向量的方向可知二面角A-A1B-C的余弦值大小为
,根据法向量的方向可知二面角A-A1B-C的余弦值大小为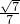
 ,得到点C到平面A1AB的距离;
,得到点C到平面A1AB的距离;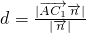 ,其中
,其中 平面A1AB的法向量,求出法向量的坐标,代入即可求出答案.
平面A1AB的法向量,求出法向量的坐标,代入即可求出答案.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案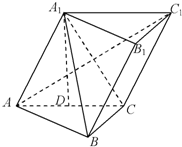 己知三棱柱ABC-A1B1C1,A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,又知BA1⊥AC1
己知三棱柱ABC-A1B1C1,A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,又知BA1⊥AC1