
【题目】设函数![]() ,
,![]() .
.
(1)当![]() (
(![]() 为自然对数的底数)时,求曲线
为自然对数的底数)时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的零点的个数;
的零点的个数;
(3)若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(I) ![]() ;(II)见解析;(III)
;(II)见解析;(III)![]() 。
。
【解析】试题分析:(1)当![]() 时,
时,![]() ,
,![]() ,由此利用导数性质能求出
,由此利用导数性质能求出![]() 的极小值;(2)由
的极小值;(2)由![]() ,得
,得![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,由此利用导数性质能求出函数
,由此利用导数性质能求出函数![]() 零点的个数;(3)当
零点的个数;(3)当![]() 时,
时,![]() 在
在![]() 上恒成立,由此能求出
上恒成立,由此能求出![]() 的取值范围.
的取值范围.
试题解析:(1)当![]() 时,
时,![]() ,所以
,所以![]() ,
, ![]() ,切点坐标为
,切点坐标为![]() 所以曲线
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(2)因为函数![]() 令
令![]() ,得
,得![]() ,设
,设![]() 所以
所以![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上为增函数;当
上为增函数;当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上为减函数,所以当
上为减函数,所以当![]() 时,
时,![]() 取极大值
取极大值![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,由函数
,由函数![]() 的图像知:
的图像知:
当![]() 时,函数
时,函数![]() 和函数
和函数![]() 无交点;
无交点;
当![]() 时,函数
时,函数![]() 和函数
和函数![]() 有且仅有一个交点;
有且仅有一个交点;
当![]() 时,函数
时,函数![]() 和函数
和函数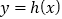 有两个交点;
有两个交点;
④当![]() 时,函数
时,函数![]() 和函数
和函数![]() 有且仅有一个交点。
有且仅有一个交点。
综上所述,当![]() 时,函数
时,函数![]() 无零点;
无零点;
当![]() 或
或![]() 时,函数
时,函数![]() 有且仅有一个零点
有且仅有一个零点
当![]() 时,函数
时,函数![]() 有两个零点
有两个零点
(3)对任意![]() 恒成立,等价于
恒成立,等价于![]() 恒成立,设
恒成立,设![]() 则
则![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上恒成立,因为
上恒成立,因为![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() 时,
时,![]() ,
,
所以实数![]() 的取值范围
的取值范围![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知A={x| ![]() <3x<9},B={x|log2x>0}.
<3x<9},B={x|log2x>0}.
(1)求A∩B和A∪B;
(2)定义A﹣B={x|x∈A且xB},求A﹣B和B﹣A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一条宽为![]() 的两平行河岸有村庄
的两平行河岸有村庄![]() 和供电站
和供电站![]() ,村庄
,村庄![]() 与
与![]() 的直线距离都是
的直线距离都是![]() ,
, ![]() 与河岸垂直,垂足为
与河岸垂直,垂足为![]() 现要修建电缆,从供电站
现要修建电缆,从供电站![]() 向村庄
向村庄![]() 供电.修建地下电缆、水下电缆的费用分别是
供电.修建地下电缆、水下电缆的费用分别是![]() 万元
万元![]() 、
、![]() 万元
万元![]() .
.
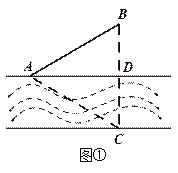
(1) 如图①,已知村庄![]() 与
与![]() 原来铺设有电缆
原来铺设有电缆![]() ,现先从
,现先从![]() 处修建最短水下电缆到达对岸后后,再修建地下电缆接入原电缆供电,试求该方案总施工费用的最小值;
处修建最短水下电缆到达对岸后后,再修建地下电缆接入原电缆供电,试求该方案总施工费用的最小值;
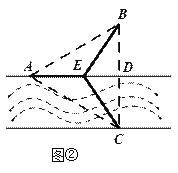
(2) 如图②,点![]() 在线段
在线段![]() 上,且铺设电缆的线路为
上,且铺设电缆的线路为![]() .若
.若![]() ,试用
,试用![]() 表示出总施工费用
表示出总施工费用![]() (万元)的解析式,并求
(万元)的解析式,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个内角A,B,C对应的边分别a,b,c,且acosC,bcosB,ccosA成等差数列,则角B等于( )
A.30°
B.60°
C.90°
D.120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com