练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设f(x)＝|log2x|在区间[a，b]上的值域为[0，2]，那么b－a的最小值为

    [　　]

    A．

    B．3

    C．

    D．

    答案：A
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：学习高手必修一数学苏教版 苏教版 题型：044

    设f(x)＝log为奇函数，a为常数．

    (1)求a的值；

    (2)证明f(x)在区间(1，＋∞)内单调递增；

    (3)若对于区间[3，4]上的每一个x的值，不等式f(x)＞()x＋m恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2010年普通高等学校招生全国统一考试、理科数学(浙江卷) 题型：013

    设函数的集合P＝{f(x)＝log(x＋a)＝b|a＝－，0，，1；b＝－1，0，1|}，平面上点的集合Q＝{(x，y)|x＝－，0，，1；y＝－1，0，1|}，则在同一直角坐标系中，P中函数f(x)的图像恰好经过Q中两个点的函数的个数是

    [　　]
    A．

    4

    B．

    6

    C．

    8

    D．

    10

    查看答案和解析>>

    科目：高中数学 来源：江西省新建二中2012届高三上学期期中考试数学文科试题 题型：013

    设函数f(x)是定义在R上以2为周期的偶函数，已知x∈(0，1)时，f(x)＝log(1－x)，则函数f(x)在(1，2)上

    [　　]
    A．

    是减函数，且f(x)＞0

    B．

    是减函数，且f(x)＜0

    C．

    是增函数，且f(x)＞0

    D．

    是增函数，且f(x)＜0

    查看答案和解析>>

    科目：高中数学 来源：2010年甘肃省高二下学期期末考试数学卷 题型：解答题

    （本小题满分12分）

     (理科)已知数列 {2 n•an} 的前 n 项和 Sn = 9－6n.

     (I)    求数列 {an} 的通项公式；

    (II)    设 bn = n·(2－log 2 )，求数列 { } 的前 n 项和Tn.

    （文科）已知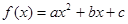，且f(0)=8及f(x+1)－f(x)＝－2x+1。

     (1)求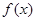的解析式；

     (2)求函数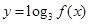的单调递减区间及值域．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数

    f(x)＝

    (1)求f(log2 )与f(log )的值；

    (2)求满足f(x)＝2的x的值；

    (3)求f(x)的最小值．

    查看答案和解析>>

    同步练习册答案