
(2009重庆卷文)(本小题满分13分,(Ⅰ)问7分,(Ⅱ)问6分)
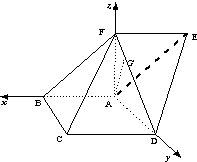
如题(18)图,在五面体![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,![]() 平面
平面![]() ,
,![]() .求:
.求:
 (Ⅰ)直线
(Ⅰ)直线![]() 到平面
到平面![]() 的距离;
的距离;
(Ⅱ)二面角![]() 的平面角的正切值.
的平面角的正切值.
解法一:
(Ⅰ)![]() 平面
平面![]() ,
, ![]() AB到面
AB到面![]() 的距离等于点A到面
的距离等于点A到面![]() 的距离,过点A作
的距离,过点A作![]() 于G,因
于G,因![]()
![]() ∥
∥![]() ,故
,故![]() ;又
;又![]()
![]() 平面
平面![]() ,由三垂线定理可知,
,由三垂线定理可知,![]() ,故
,故![]() ,知
,知![]() ,所以AG为所求直线AB到面
,所以AG为所求直线AB到面![]() 的距离。
的距离。
在![]() 中,
中,![]()
由![]() 平面
平面![]() ,得
,得![]() AD,从而在
AD,从而在![]() 中,
中,![]()
![]()
![]() 。即直线
。即直线![]() 到平面
到平面![]() 的距离为
的距离为![]() 。
。
(Ⅱ)由己知,![]() 平面
平面![]() ,得
,得![]() AD,又由
AD,又由![]() ,知
,知![]() ,故
,故![]() 平面ABFE
平面ABFE
![]()
![]() ,所以,
,所以,![]() 为二面角
为二面角![]() 的平面角,记为
的平面角,记为![]() .
.
在![]() 中,
中, ![]() ,由
,由![]() 得,
得,![]() ,从而
,从而![]()
在![]() 中,
中, ![]() ,故
,故![]()
 所以二面角
所以二面角![]() 的平面角的正切值为
的平面角的正切值为![]() .
.
解法二:
(Ⅰ)如图以A点为坐标原点,![]() 的方向为
的方向为![]() 的正方向建立空间直角坐标系数,则
的正方向建立空间直角坐标系数,则
A(0,0,0) C(2,2,0) D(0,2,0) 设![]() 可得
可得![]() ,由
,由![]() .即
.即![]() ,解得
,解得![]()
![]()
![]() ∥
∥![]() ,
,
![]() 面
面![]() ,所以直线AB到面
,所以直线AB到面![]() 的距离等于点A到面
的距离等于点A到面![]() 的距离。设A点在平面
的距离。设A点在平面![]() 上的射影点为
上的射影点为![]() ,则
,则![]() 因
因![]() 且
且![]() ,而
,而![]()
![]() ,此即
,此即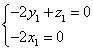 解得
解得![]() ① ,知G点在
① ,知G点在![]() 面上,故G点在FD上.
面上,故G点在FD上.
![]() ,
,![]() 故有
故有![]() ② 联立①,②解得,
② 联立①,②解得, ![]() .
.
![]()
![]() 为直线AB到面
为直线AB到面![]() 的距离. 而
的距离. 而![]() 所以
所以![]()
(Ⅱ)因四边形![]() 为平行四边形,则可设
为平行四边形,则可设![]() ,
,![]() .由
.由
![]() 得
得![]() ,解得
,解得![]() .即
.即![]() .故
.故![]()
由![]() ,
,![]() 因
因![]() ,
,![]() ,故
,故![]() 为二面角
为二面角![]() 的平面角,又
的平面角,又![]()
![]() ,
,![]() ,
,![]() ,所以
,所以![]()


科目:高中数学 来源: 题型:
17.(2009重庆卷文)从一堆苹果中任取5只,称得它们的质量如下(单位:克)125 124 121 123 127则该样本标准差![]() (克)(用数字作答).
(克)(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009重庆卷文)(本小题满分13分,(Ⅰ)问7分,(Ⅱ)问6分)
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为![]() 和
和![]() ,且各株大树是否成活互不影响.求移栽的4株大树中:w.w.w.k.s.5.u.c.o.m
,且各株大树是否成活互不影响.求移栽的4株大树中:w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅰ)至少有1株成活的概率;
(Ⅱ)两种大树各成活1株的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009重庆卷文)在正四棱柱![]() 中,顶点
中,顶点![]() 到对角线
到对角线![]() 和到平面
和到平面![]() 的距离分别为
的距离分别为![]() 和
和![]() ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.若侧棱的长小于底面的变长,则![]() 的取值范围为
的取值范围为![]()
B.若侧棱的长小于底面的变长,则![]() 的取值范围为
的取值范围为![]()
C.若侧棱的长大于底面的变长,则![]() 的取值范围为
的取值范围为![]()
D.若侧棱的长大于底面的变长,则![]() 的取值范围为
的取值范围为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009重庆卷文)在正四棱柱![]() 中,顶点
中,顶点![]() 到对角线
到对角线![]() 和到平面
和到平面![]() 的距离分别为
的距离分别为![]() 和
和![]() ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.若侧棱的长小于底面的变长,则![]() 的取值范围为
的取值范围为![]()
B.若侧棱的长小于底面的变长,则![]() 的取值范围为
的取值范围为![]()
C.若侧棱的长大于底面的变长,则![]() 的取值范围为
的取值范围为![]()
D.若侧棱的长大于底面的变长,则![]() 的取值范围为
的取值范围为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com