
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)将函数![]() 的图象做怎样的平移变换可以得到函数
的图象做怎样的平移变换可以得到函数![]() 的图象;
的图象;
(Ⅲ)若方程![]() 在
在![]() 上有两个不相等的实数根,求
上有两个不相等的实数根,求![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)沿
;(II)沿![]() 轴向左平移
轴向左平移![]() (III)
(III)![]()
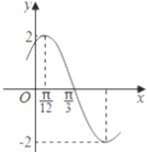
【解析】试题分析:(Ⅰ)根据图象得A=2,T=π,故可得ω=2,所以f(x)=2sin(2x+φ),又点(![]() ,2)在函数的图象上,从而得到φ=
,2)在函数的图象上,从而得到φ=![]() ,所以
,所以![]() 。(Ⅱ)由于y= =2sin[2(x﹣
。(Ⅱ)由于y= =2sin[2(x﹣![]() )],f(x)=2sin[2(x﹣
)],f(x)=2sin[2(x﹣ ![]() +
+![]() )],因此可得将函数y=
)],因此可得将函数y=![]() sin2x﹣cos2x的图象沿x轴向左平移
sin2x﹣cos2x的图象沿x轴向左平移![]() 可以得到函数f(x)的图象。(Ⅲ)画出函数
可以得到函数f(x)的图象。(Ⅲ)画出函数![]() 在
在![]() 上图象,结合图象求解即可。
上图象,结合图象求解即可。
试题解析:
(1)根据图象得A=2,![]() =
=![]() ﹣
﹣![]() =
=![]() ,
,
∴T=π,
由![]() =π,可得ω=2,
=π,可得ω=2,
∴f(x)=2sin(2x+φ),
又点(![]() ,2)在函数的图象上,
,2)在函数的图象上,
∴2sin(![]() +φ)=2,
+φ)=2,
∵|φ|<![]() ,
,
∴φ=![]() ,
,
∴f(x)=2sin(2x+![]() ).
).
(2)∵y=![]() sin2x﹣cos2x=2sin(2x﹣
sin2x﹣cos2x=2sin(2x﹣![]() )=2sin[2(x﹣
)=2sin[2(x﹣![]() )],
)],
又f(x)=2sin(2x+![]() )=2sin[2(x+
)=2sin[2(x+![]() )]=2sin[2(x﹣
)]=2sin[2(x﹣ ![]() +
+![]() )],
)],
∴将函数y=![]() sin2x﹣cos2x的图象沿x轴向左平移
sin2x﹣cos2x的图象沿x轴向左平移![]() 可以得到函数f(x)的图象。
可以得到函数f(x)的图象。
(3)∵![]() ,
,
∴![]() 。
。
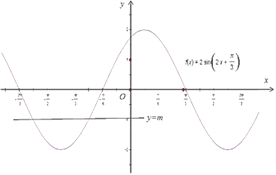
画出函数![]() 在
在![]() 上图象如图所示。
上图象如图所示。
结合函数的图象可得若方程f(x)=m在区间[﹣![]() ,0]内有两个不相等的实数根,
,0]内有两个不相等的实数根,
则![]() 。
。
∴要有两个不相等的实根,实数m的取值范围为![]() 。
。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为θ= ![]() ,曲线C的参数方程为
,曲线C的参数方程为 ![]() .
.
(1)写出直线l与曲线C的直角坐标方程;
(2)过点M平行于直线l1的直线与曲线C交于A、B两点,若|MA||MB|= ![]() ,求点M轨迹的直角坐标方程.
,求点M轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC= ![]() .等边三角形ADB以AB为轴运动.
.等边三角形ADB以AB为轴运动. 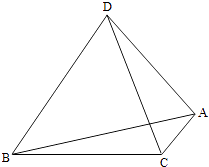
(1)当平面ADB⊥平面ABC时,求CD;
(2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知二面角α﹣MN﹣β的大小为60°,菱形ABCD在面β内,A、B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥面α,垂足为O. 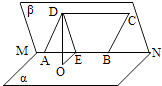
(1)证明:AB⊥平面ODE;
(2)求异面直线BC与OD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD﹣A1B1C1D1为正方体,下面结论错误的是( ) 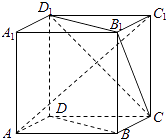
A.BD∥平面CB1D1
B.AC1⊥BD
C.异面直线AD与CB1角为60°
D.AC1⊥平面CB1D1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,建立空间直角坐标系Dxyz,已知正方体ABCD﹣A1B1C1D1的棱长为1,点M是正方体对角线D1B的中点,点N在棱CC1上. 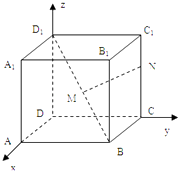
(1)当2|C1N|=|NC|时,求|MN|;
(2)当点N在棱CC1上移动时,求|MN|的最小值并求此时的N点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点![]() 的椭圆
的椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
, ![]() 为椭圆上的任意一点,且
为椭圆上的任意一点,且![]() 成等差数列.
成等差数列.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆于
交椭圆于![]() 两点,若点
两点,若点![]() 始终在以
始终在以![]() 为直径的圆外,求实数
为直径的圆外,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com