解:(1)∵点A在圆x
2+y
2=c
2上,
∴△AF
1F
2为一直角三角形,
∵
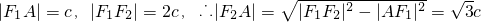
由椭圆的定义知:|AF
1|+|AF
2|=2a,∴c+2

c=2a
∴e=

=
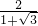
=

-1
(2)∵函数
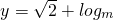
x的图象恒过点
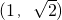
∴
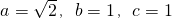
,
点F
1(-1,0),F
2(1,0),
①若AB⊥x轴,则A
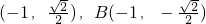
,
∴
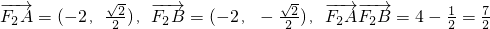
②若AB与x轴不垂直,设直线AB的斜率为k,则AB的方程为y=k(x+1)
由
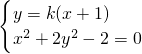
消去y得(1+2k
2)x
2+4k
2x+2(k
2-1)=0(*)
∵△=8k
2+8>0,∴方程(*)有两个不同的实根.
设点A(x
1,y
1),B(x
2,y
2),
则x
1,x
2是方程(*)的两个根
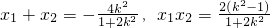
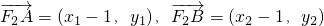
,
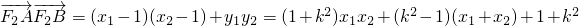
=
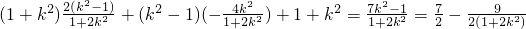
∵
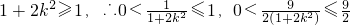
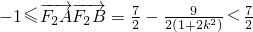
,
由①②知
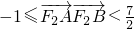
.
分析:(1)根据题意判断出∴△AF
1F
2为一直角三角形,利用勾股定理求得|F
2A|利用椭圆的定义求得|AF
1|+|AF
2|=2a,进而求得a和c的关系,则椭圆的离心率可得.
(2)利用函数的图象恒过定点,求得a和b,则c可求得,求得椭圆的两焦点,先看AB⊥x轴时,求得A,B的坐标,进而求得

的坐标,则
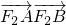
可求得;再看AB与x轴不垂直,设直线AB的方程,与椭圆的方程联立消去y,利用判别式求得k的范围,设出A,B的坐标,进而表示出x
1+x
2和x
1x
2,

的坐标进而求得
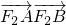
的表达式,利用k的范围确定
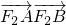
的范围.
点评:本题主要考查了直线与圆锥曲线的综合问题.涉及了椭圆的基本性质,向量的运算,考查了知识的综合运用和基本的运算能力.

 的左、右焦点分别为F1、F2,过F1的直线l与椭圆交于A、B两点.
的左、右焦点分别为F1、F2,过F1的直线l与椭圆交于A、B两点.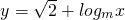 ,(m>0且m≠1)的图象,无论m为何值时恒过定点(b,a),求
,(m>0且m≠1)的图象,无论m为何值时恒过定点(b,a),求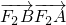 的取值范围.
的取值范围.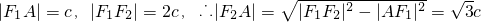
 c=2a
c=2a =
=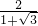 =
= -1
-1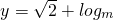 x的图象恒过点
x的图象恒过点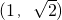
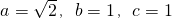 ,
,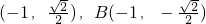 ,
,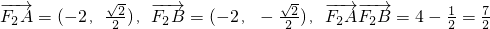
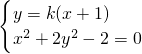 消去y得(1+2k2)x2+4k2x+2(k2-1)=0(*)
消去y得(1+2k2)x2+4k2x+2(k2-1)=0(*)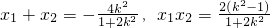
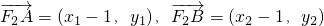 ,
,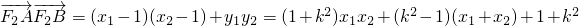
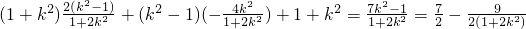
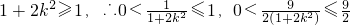
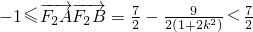 ,
,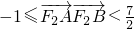 .
. 的坐标,则
的坐标,则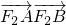 可求得;再看AB与x轴不垂直,设直线AB的方程,与椭圆的方程联立消去y,利用判别式求得k的范围,设出A,B的坐标,进而表示出x1+x2和x1x2,
可求得;再看AB与x轴不垂直,设直线AB的方程,与椭圆的方程联立消去y,利用判别式求得k的范围,设出A,B的坐标,进而表示出x1+x2和x1x2, 的坐标进而求得
的坐标进而求得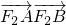 的表达式,利用k的范围确定
的表达式,利用k的范围确定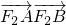 的范围.
的范围.

 的左、右焦点分别为F1、F2,其中F2也是抛物线
的左、右焦点分别为F1、F2,其中F2也是抛物线 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
 上,求直线AC的方程。
上,求直线AC的方程。