
【题目】如图,C、D是离心率为![]() 的椭圆的左、右顶点,
的椭圆的左、右顶点,![]() 、
、![]() 是该椭圆的左、右焦点, A、B是直线
是该椭圆的左、右焦点, A、B是直线![]() 4上两个动点,连接AD和BD,它们分别与椭圆交于点E、F两点,且线段EF恰好过椭圆的左焦点
4上两个动点,连接AD和BD,它们分别与椭圆交于点E、F两点,且线段EF恰好过椭圆的左焦点![]() . 当
. 当![]() 时,点E恰为线段AD的中点.
时,点E恰为线段AD的中点.
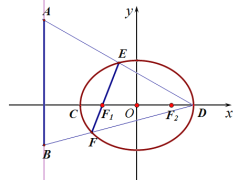
(Ⅰ)求椭圆的方程;
(Ⅱ)求证:以AB为直径的圆始终与直线EF相切.
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)如图,四棱锥![]() 的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连结
的中点,连结![]() .求证:
.求证:
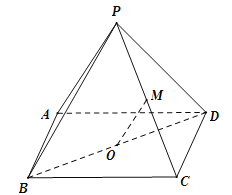
(1)![]() ∥平面
∥平面![]() ;
;
(2)![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若函数
,若函数![]() 满足:①在区间
满足:①在区间![]() 上单调递减;②存在常数
上单调递减;②存在常数![]() ,使其值域为
,使其值域为![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的“渐近函数”.
的“渐近函数”.
(1)求证:函数![]() 不是函数
不是函数![]() 的“渐近函数”;
的“渐近函数”;
(2)判断函数![]() 是不是函数
是不是函数![]() ,
,![]() 的“渐近函数”,并说明理由;
的“渐近函数”,并说明理由;
(3)若函数![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() 是函数
是函数![]() 的“渐近函数”充要条件是
的“渐近函数”充要条件是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在第十五次全国国民阅读调查中,某地区调查组获得一个容量为![]() 的样本,其中城镇居民
的样本,其中城镇居民![]() 人,农村居民
人,农村居民![]() 人.在这些居民中,经常阅读的城镇居民
人.在这些居民中,经常阅读的城镇居民![]() 人,农村居民
人,农村居民![]() 人.
人.
(Ⅰ)填写下面列联表,并判断是否有![]() 的把握认为,经常阅读与居民居住地有关?
的把握认为,经常阅读与居民居住地有关?
城镇居民 | 农村居民 | 合计 | |
经常阅读 |
|
| |
不经常阅读 | |||
合计 |
|
(Ⅱ)从该地区居民城镇的居民中,随机抽取![]() 位居民参加一次阅读交流活动,记这
位居民参加一次阅读交流活动,记这![]() 位居民中经常阅读的人数为
位居民中经常阅读的人数为![]() ,若用样本的频率作为概率,求随机变量
,若用样本的频率作为概率,求随机变量![]() 的分布列和期望.
的分布列和期望.
附: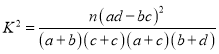 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】地球海洋面积远远大于陆地面积,随着社会的发展,科技的进步,人类发现海洋不仅拥有巨大的经济利益,还拥有着深远的政治利益.联合国于第63届联合国大会上将每年的6月8日确定为“世界海洋日”.2019年6月8日,某大学的行政主管部门从该大学随机抽取100名大学生进行一次海洋知识测试,并按测试成绩(单位:分)分组如下:第一组[65,70),第二组[70,75),第二组[75,80),第四组[80,85),第五组[85,90],得到频率分布直方图如下图:
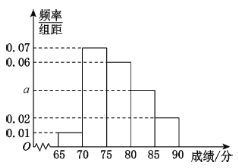
(1)求实数![]() 的值;
的值;
(2)若从第四组、第五组的学生中按组用分层抽样的方法抽取6名学生组成中国海洋实地考察小队,出发前,用简单随机抽样方法从6人中抽取2人作为正、副队长,列举出所有的基本事件并求“抽取的2人为不同组”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面上给定相异两点A,B,设P点在同一平面上且满足![]() ,当
,当![]() 且
且![]() 时,P点的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故我们称这个圆为阿波罗尼斯圆,现有双曲线
时,P点的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故我们称这个圆为阿波罗尼斯圆,现有双曲线![]() (
(![]() ,
,![]() ),A,B为双曲线的左、右顶点,C,D为双曲线的虚轴端点,动点P满足
),A,B为双曲线的左、右顶点,C,D为双曲线的虚轴端点,动点P满足 ,
,![]() 面积的最大值为
面积的最大值为![]() ,
,![]() 面积的最小值为4,则双曲线的离心率为______.
面积的最小值为4,则双曲线的离心率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的方程为
的方程为![]() ,且圆
,且圆![]() 与
与![]() 轴交于
轴交于![]() 两点,设直线
两点,设直线![]() 的方程为
的方程为![]() .
.
(1)当直线![]() 与圆
与圆![]() 相切时,求直线
相切时,求直线![]() 的方程;
的方程;
(2)已知直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点.(i)
两点.(i)![]() ,求直线
,求直线![]() 的方程;(ii)直线
的方程;(ii)直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,是否存在常数
,是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )经过点
)经过点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 有两个不同的交点
有两个不同的交点![]() 、
、![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() .
.
(1)若直线![]() 过点
过点![]() ,求直线
,求直线![]() 的斜率的取值范围;
的斜率的取值范围;
(2)若直线![]() 过点
过点![]() ,设
,设![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com