
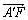
(1)求证:A′F⊥C′E;
(2)当三棱锥B′—BEF的体积取得最大值时,求二面角B′—EF—B的大小.(结果用反三角函数表示)
19.(1)[证明]如图,以O为原点建立空间直角坐标系.

设AE=BF=x,则A′(a,0,a)、F(a-x,a,0)、C′(0,a,a)、
E(a,x,0), ![]() =(-x,a,-a),
=(-x,a,-a),![]() =(a,x-a,-a).
=(a,x-a,-a).
∵![]() ·
·![]() =-xa+a(x-a)+a2=0,
=-xa+a(x-a)+a2=0,
∴A′F⊥C′E.
(2)[解]记BF=x,BE=y,则x+y=a,三棱锥B′—BEF的体积V=![]() xya≤
xya≤![]()
![]() =
=![]() a3,
a3,
当且仅当x=y=![]() 时,等号成立.
时,等号成立.
因此,三棱锥B′—BEF的体积取得最大值时,BE=BF=![]() .
.
过B作BD⊥EF交EF于D,连B′D,可知B′D⊥EF.
∴∠B′DB是二面角B′—EF—B的平面角.
在直角三角形BEF中,直角边BE=BF=![]() ,BD是斜边上的高,
,BD是斜边上的高,
∴BD=![]() a.
a.
tanB′DB=![]() =2
=2![]() ,
,
故二面角B′—EF—B的大小为arctan2![]() .
.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:高中数学 来源: 题型:
 (甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=2
(甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=2| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
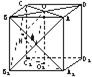 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、O、O1分别是A1B、AC、A1C1的中点,且OH⊥O1B,垂足为H.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、O、O1分别是A1B、AC、A1C1的中点,且OH⊥O1B,垂足为H.查看答案和解析>>
科目:高中数学 来源: 题型:
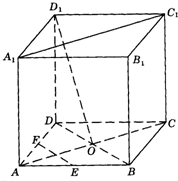 如图,在棱长为a的正方体ABCD-A1B1C1D1中,O是AC、BD的交点,E,F分别是AB与AD的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,O是AC、BD的交点,E,F分别是AB与AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2001•上海)在棱长为a的正方体OABC-O′A′B′C′中,E、F分别是棱AB、BC上的动点,且AE=BF.
(2001•上海)在棱长为a的正方体OABC-O′A′B′C′中,E、F分别是棱AB、BC上的动点,且AE=BF.查看答案和解析>>
科目:高中数学 来源:上海 题型:解答题
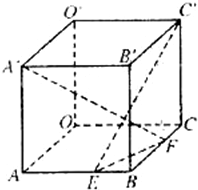
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com