
【题目】如图,四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() 为线段
为线段![]() 上一点,
上一点, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)证明: ![]()
(2)求四面体![]() 的体积.
的体积.

【答案】(1)见解析(2)![]()
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,证得
,证得![]() ,得出
,得出![]() ,
,
即![]() ,再用线面平行的判定定理,即可作出证明;
,再用线面平行的判定定理,即可作出证明;
(2)根据题意,得出![]() 到
到![]() 的距离为,得出
的距离为,得出![]() ,再利用三棱锥的体积公式,即可求得三棱锥的体积.
,再利用三棱锥的体积公式,即可求得三棱锥的体积.
试题解析:
(1)证明:由已知得AM=![]() AD=2,如图,取BP的中点T,连接AT,TN,由N为PC中点知TN∥BC,TN=
AD=2,如图,取BP的中点T,连接AT,TN,由N为PC中点知TN∥BC,TN=![]() BC=2.又AD∥BC,故
BC=2.又AD∥BC,故![]() ,所以四边形AMNT为平行四边形,
,所以四边形AMNT为平行四边形,
于是MN∥AT.因为AT平面PAB,MN平面PAB,所以MN∥平面PAB.
(2)因为PA⊥平面ABCD,N为PC的中点,所以N到平面ABCD的距离为![]() PA.
PA.
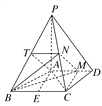
如图,取BC的中点E,连接AE,由AB=AC=3得AE⊥BC,AE=![]() =
=![]() .
.
由AM∥BC得M到BC的距离为![]() ,故S△BCM=
,故S△BCM=![]() ×4×
×4×![]() =2
=2![]() ,
,
所以四面体N-BCM的体积VN-BCM=![]() ×S△BCM×
×S△BCM×![]() =
=![]() .
.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
【题目】某市垃圾处理站每月的垃圾处理成本![]() (元)与月垃圾处理量
(元)与月垃圾处理量![]() (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为![]() ,求该站每月垃圾处理量为多少吨时,才能使每吨垃圾的平均处理成本最低?最低平均处理成本是多少?
,求该站每月垃圾处理量为多少吨时,才能使每吨垃圾的平均处理成本最低?最低平均处理成本是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若对定义域内的任意![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的值;
的值;
(2)若函数![]() 的定义域上是单调函数,求实数
的定义域上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,证明对任意的正整数
,证明对任意的正整数![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体中,四边形ABCD为菱形,对角线AC与BD的交点为O,四边形DCEF为梯形,EF∥DC,FD=FB.
(Ⅰ)若DC=2EF,求证:OE∥平面ADF;
(Ⅱ)求证:平面AFC⊥平面ABCD;
(Ⅲ)若AB=FB=2,AF=3,∠BCD=60°,求AF与平面ABCD所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,其前
,其前![]() 项和为
项和为![]() .
.
(1)若对任意的![]() ,
, ![]() ,
, ![]() ,
, ![]() 组成公差为4的等差数列,且
组成公差为4的等差数列,且![]() ,求
,求![]() ;
;
(2)若数列 是公比为
是公比为![]() (
(![]() )的等比数列,
)的等比数列, ![]() 为常数,
为常数,
求证:数列![]() 为等比数列的充要条件为
为等比数列的充要条件为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·鸡西一模)在正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,M,N分别为AB,BC中点,点Q为平面ABCD内一点,线段D1Q与OP互相平分,则满足![]() 的实数λ的值有( )
的实数λ的值有( )
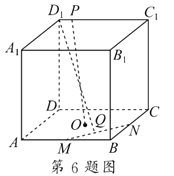
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=![]() x3-kx,其中实数k为常数.
x3-kx,其中实数k为常数.
(1)当k=4时,求函数的单调区间;
(2)若曲线y=f(x)与直线y=k只有一个交点,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com