
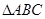 中,D,E,F分别是AB,AC和BC边的中点,
中,D,E,F分别是AB,AC和BC边的中点,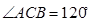 ,
,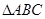 沿CD翻折成直二面角A-DC-B.(如图(2))
沿CD翻折成直二面角A-DC-B.(如图(2))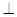 DE?证明你的结论.
DE?证明你的结论.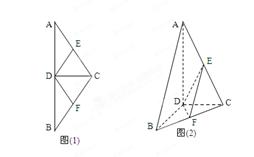
 平面DEF,EF
平面DEF,EF 平面DEF,∴AB∥平面DEF.………………4分
平面DEF,∴AB∥平面DEF.………………4分 , △DFC中,设底边DF上的高为h由
, △DFC中,设底边DF上的高为h由 ,∴h=
,∴h= 在Rt△EMN中,EM=
在Rt△EMN中,EM= ,MN=
,MN= h=
h= ,
, ……8分
……8分 则A(0,0,
则A(0,0, ),B(
),B( ,0,0),
,0,0), .…… 5分
.…… 5分 设平面EDF的法向量为
设平面EDF的法向量为 ,
, 得
得 …6分
…6分 ……7分
……7分 ……8分
……8分 ,
, ,……… 9分
,……… 9分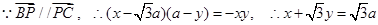 ……11分
……11分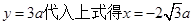 ,可知点P在BC的延长线上
,可知点P在BC的延长线上

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:单选题

| A.①②③ | B.①③ | C.①②③④ | D.①③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,
, 是两个不同的平面, m,n是两条不重合的直线,下列命题中正确的是
是两个不同的平面, m,n是两条不重合的直线,下列命题中正确的是A.若m∥ , , ∩ ∩ =n,则m∥n =n,则m∥n |
B.若m⊥ ,m⊥n,则n∥ ,m⊥n,则n∥ |
C.若m⊥ ,n⊥ ,n⊥ , , ⊥ ⊥ ,则m⊥n ,则m⊥n |
D.若 ⊥ ⊥ , , ∩ ∩ =n,m⊥n,则m⊥ =n,m⊥n,则m⊥ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.直线  平面 平面 ,平面 ,平面 //直线 //直线 ,则 ,则   |
B.平面   ,直线 ,直线 ,则 ,则 // // |
C.直线 是平面 是平面 的一条斜线,且 的一条斜线,且   ,则 ,则 与 与 必不垂直 必不垂直 |
| D.一个平面内的两条直线与另一个平面内的两条直线分别平行,则这两个平面平行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com