Question

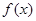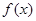对于函数，若存在x₀∈R，使方程成立，则称x₀为的不动点，已知函数（a≠0）．

（1）当时，求函数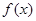的不动点；

（2）若对任意实数b，函数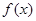恒有两个相异的不动点，求a的取值范围；

 

Answer 1

【答案】

(1) 1为的不动点(2)

【解析】

试题分析：解：（1）由题得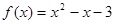：，因为为不动点，

因此有，即       2分

所以或，即3和－1为的不动点。        5分

（2）因为恒有两个不动点，

∴　，

即　（※）恒有两个不等实数根，    8分

由题设恒成立，    10分

即对于任意b∈R，有恒成立，

所以有　，    12分

　∴　　       13分

考点：本题考查的重点是函数与方程的综合运用，主要是考查了函数的零点的变形运用问题，属于基础题。考查同学们的等价转换能力和分析问题解决问题的能力。

点评：解题的关键是对新定义的理解，建立方程，将不动点的问题，转化为结合一元二次方程中必然有两个不等的实数根来求解参数的取值范围。