
已知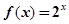
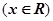 可以表示为一个奇函数
可以表示为一个奇函数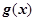 与一个偶函数
与一个偶函数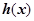 之和,若不等式
之和,若不等式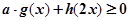 对于
对于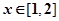 恒成立,则实数
恒成立,则实数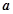 的取值范围是____________.
的取值范围是____________.
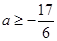
【解析】
试题分析:依题意,g(x)+h(x)=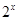 .....(1),∵g(x)是奇函数,∴g(-x)=-g(x);∵h(x)是偶函数,∴h(-x)=h(x);
.....(1),∵g(x)是奇函数,∴g(-x)=-g(x);∵h(x)是偶函数,∴h(-x)=h(x);
∴g(-x)+h(-x)=h(x)-g(x)=
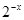 ......(2)
......(2)
解(1)和(2)组成的方程组得h(x)=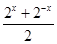 ,g(x)=
,g(x)= 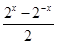
∴ag(x)+h(2x)=a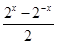 +
+ ,∴a·
,∴a·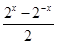 +
+ ≥0在x∈[1,2]恒成立
≥0在x∈[1,2]恒成立
令t=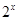 ,∴
,∴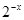 =
=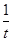 ,当x∈[1,2]时,t∈[2,4],
,当x∈[1,2]时,t∈[2,4],
∴原不等式化为a(t-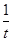 )+(t2+
)+(t2+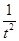 )≥0在t∈[2,4]上恒成立,由不等式a(t-
)≥0在t∈[2,4]上恒成立,由不等式a(t-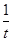 )+(t2+
)+(t2+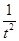 )≥0,
)≥0,
可得a(t-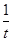 )≥-(t2+
)≥-(t2+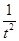 ),∵当t∈[2,4]时,t-
),∵当t∈[2,4]时,t-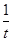 t>0恒成立,∴a≥
t>0恒成立,∴a≥ =
= =
=
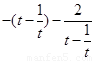 ,即a≥
,即a≥ 在t∈[2,4]上恒成立,
在t∈[2,4]上恒成立,
令u=t-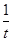 ,求导得
,求导得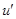 =1+
=1+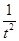 >0恒成立,∴u=t-
>0恒成立,∴u=t-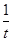 在t∈[2,4]上单调递增
在t∈[2,4]上单调递增
∴u∈[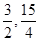 ],令f(u)=u+
],令f(u)=u+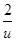 ,u∈[
,u∈[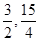 ],
],
求导得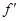 (u)=1-
(u)=1-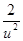 >0在u∈[
>0在u∈[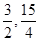 ]上恒成立,∴f(u)在u∈[
]上恒成立,∴f(u)在u∈[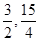 ]上单调递增
]上单调递增
即当u=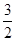 ,f(u)取最小值f(
,f(u)取最小值f(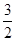 )=
)=
 ,
,
当u=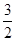 时,可解得t=2(另一根不在t∈[2,4]内故舍去)
时,可解得t=2(另一根不在t∈[2,4]内故舍去)
∴当t=2时, 取最小值为
取最小值为 ,即
,即 取最大值为-
取最大值为- ,∴a≥-
,∴a≥- ,当t=2,x=1时取等号,∴a的最小值为-
,当t=2,x=1时取等号,∴a的最小值为- .
.
考点:1.函数的奇偶性;2.不等式的性质;3.导数的性质.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 17 |
| 6 |
| 17 |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省哈尔滨三中高三(上)9月月考数学试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省荆州市公安三中高三(上)数学积累测试卷07(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com