
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)已知![]() 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当![]() 时,有
时,有![]() .若
.若![]() ,且
,且![]() ,求函数
,求函数![]()
![]() 的反函数;
的反函数;
(3)若在![]() 上存在
上存在![]() 个不同的点
个不同的点![]() ,
,![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)直接利用绝对值不等式的解法及应用求出结果.
(2)利用函数的周期和函数的关系式的应用求出函数的反函数.
(3)利用绝对值不等式的应用和函数的性质的应用,利用分类讨论思想的应用求出结果.
解:(1)解不等式![]()
当![]() 时,
时,![]() ,所以
,所以![]()
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
综上,该不等式的解集为![]()
(2)当![]() 时,
时,![]() ,
,
因为![]() 是以2为周期的偶函数,
是以2为周期的偶函数,
所以![]() ,
,
由![]() ,且
,且![]() ,得
,得![]() ,
,
所以当![]() 时,
时,![]()
所以当![]() 时,
时,
![]() ,
,
所以函数![]() 的反函数为
的反函数为
![]()
(3)①当![]() 时,在
时,在![]() 上
上![]() ,是
,是![]() 上的增函数,所以
上的增函数,所以
![]()
所以![]() ,得
,得![]() ;
;
②当![]() 时,在
时,在![]() 上
上![]() ,是
,是![]() 上的增函数,所以
上的增函数,所以
![]()
所以![]() ,得
,得![]() ;
;
③当![]() 时,
时,![]() 在
在![]() 上不单调,所以
上不单调,所以
![]()
![]() ,
,![]() ,
,
在![]() 上,
上,![]() .
.
![]() ,不满足.
,不满足.
综上,![]() 的取值范围为
的取值范围为![]() .
.
③当![]() 时,则
时,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,于是
上单调递减,于是![]()
![]()
令![]() ,解得
,解得![]() 或
或![]() ,不符合题意;
,不符合题意;
④当![]() 时,
时,![]() 分别在
分别在![]() 、
、![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
![]()
![]()
![]()
令![]() ,解得
,解得![]() 或
或![]() ,不符合题意.
,不符合题意.
综上,所求实数![]() 的取值范围为
的取值范围为![]() .
.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】为推进“千村百镇计划”,![]() 年
年![]() 月某新能源公司开展“电动莆田 绿色出行”活动,首批投放
月某新能源公司开展“电动莆田 绿色出行”活动,首批投放![]() 台
台![]() 型新能源车到莆田多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对
型新能源车到莆田多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对![]() 型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为
型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为![]() 分).最后该公司共收回
分).最后该公司共收回![]() 份评分表,现从中随机抽取
份评分表,现从中随机抽取![]() 份(其中男、女的评分表各
份(其中男、女的评分表各![]() 份)作为样本,经统计得到如下茎叶图:
份)作为样本,经统计得到如下茎叶图:

(1)求![]() 个样本数据的中位数
个样本数据的中位数![]() ;
;
(2)已知![]() 个样本数据的平均数
个样本数据的平均数![]() ,记
,记![]() 与
与![]() 的最大值为
的最大值为![]() .该公司规定样本中试用者的“认定类型”:评分不小于
.该公司规定样本中试用者的“认定类型”:评分不小于![]() 的为“满意型”,评分小于
的为“满意型”,评分小于![]() 的为“需改进型”.
的为“需改进型”.
①请根据![]() 个样本数据,完成下面
个样本数据,完成下面![]() 列联表:
列联表:
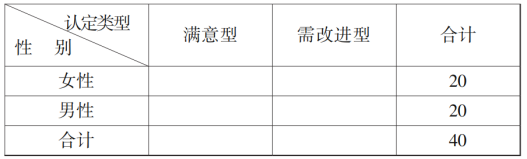
根据![]() 列联表判断能否有
列联表判断能否有![]() 的把握认为“认定类型”与性别有关?
的把握认为“认定类型”与性别有关?
②为做好车辆改进工作,公司先从样本“需改进型”的试用者按性别用分层抽样的方法,从中抽取8人进行回访,根据回访意见改进车辆后,再从这8人中随机抽取3人进行二次试用,记这3人中男性人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
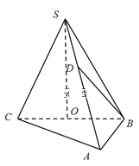
【题目】在三棱锥![]() 中,底面是边长为
中,底面是边长为![]() 的正三角形,点
的正三角形,点![]() 在底面
在底面![]() 上的射影
上的射影![]() 恰是
恰是![]() 的中点,侧棱
的中点,侧棱![]() 和底面成
和底面成![]() 角.
角.
(1)若![]() 为侧棱
为侧棱![]() 上一点,当
上一点,当![]() 为何值时,
为何值时,![]() ;
;
(2)求二面角![]() 的余弦值大小.
的余弦值大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现定义:设![]() 是非零实常数,若对于任意的
是非零实常数,若对于任意的![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“关于的
为“关于的![]() 偶型函数”
偶型函数”
(1)请以三角函数为例,写出一个“关于2的偶型函数”的解析式,并给予证明
(2)设定义域为的“关于的![]() 偶型函数”在区间
偶型函数”在区间![]() 上单调递增,求证在区间
上单调递增,求证在区间![]() 上单调递减
上单调递减
(3)设定义域为![]() 的“关于
的“关于![]() 的偶型函数”
的偶型函数”![]() 是奇函数,若
是奇函数,若![]() ,请猜测
,请猜测![]() 的值,并用数学归纳法证明你的结论
的值,并用数学归纳法证明你的结论
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】至![]() 年底,我国发明专利申请量已经连续
年底,我国发明专利申请量已经连续![]() 年位居世界首位,下表是我国
年位居世界首位,下表是我国![]() 年至
年至![]() 年发明专利申请量以及相关数据.
年发明专利申请量以及相关数据.
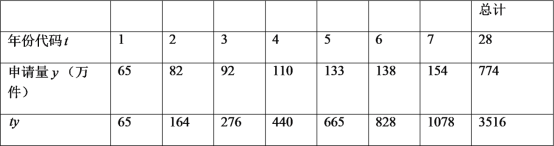
注:年份代码![]() ~
~![]() 分别表示
分别表示![]() ~
~![]() .
.
(1)可以看出申请量每年都在增加,请问这几年中哪一年的增长率达到最高,最高是多少?
(2)建立![]() 关于
关于![]() 的回归直线方程(精确到
的回归直线方程(精确到![]() ),并预测我国发明专利申请量突破
),并预测我国发明专利申请量突破![]() 万件的年份.
万件的年份.
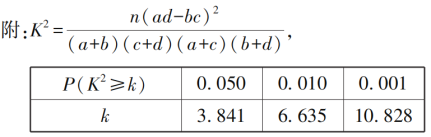
参考公式:回归直线的斜率和截距的最小二乘法估计分别为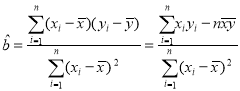 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且AB=1,BC=2, ∠ABC=60°,PA⊥平面ABCD,AE⊥PC于E,
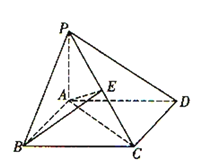
下列四个结论:①AB⊥AC;②AB⊥平面PAC;③PC⊥平面ABE;④BE⊥PC.正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com