
如图3-1.已知![]() 、
、![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 和棱
和棱![]() 的中点.
的中点.
(Ⅰ)试判断四边形![]() 的形状;
的形状;
(Ⅱ)求证:平面![]() 平面
平面![]() .
.

 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:
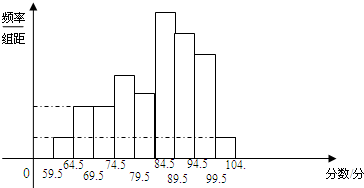 为了了解某校毕业班数学考试情况,抽取了若干名学生的数学成绩,将所得的数据经过整理后,画出频率分布直方图(如图所示).已知从左到右第一组的频率是0.03,第二组的频率是0.06,第四组的频率是0.12,第五组的频率是0.10,第六组的频率是0.27,且第四组的频数是12,则
为了了解某校毕业班数学考试情况,抽取了若干名学生的数学成绩,将所得的数据经过整理后,画出频率分布直方图(如图所示).已知从左到右第一组的频率是0.03,第二组的频率是0.06,第四组的频率是0.12,第五组的频率是0.10,第六组的频率是0.27,且第四组的频数是12,则查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
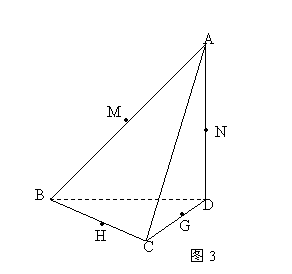
如图3所示,已知三棱锥![]() 中,
中,![]() 点
点![]()
![]() 的中点.
的中点.
(1)求证![]() 四点共面;
四点共面;
(2)已知![]() ,点C在球面上,求球M的体积V.
,点C在球面上,求球M的体积V.

查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
如图3所示,已知三棱锥![]() 中,
中,![]() 点
点![]()
![]() 的中点.
的中点.
(1)求证![]() 四点共面;
四点共面;
(2)已知![]() ,点C在球面上,求球M的体积V.
,点C在球面上,求球M的体积V.


查看答案和解析>>
科目:高中数学 来源:上海市黄浦区2010届高三上学期期终基础学业测评(数学理) 题型:解答题
本题共有2个小题,第1小题满分7分,第2小题满分7分.
|
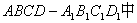 ,
,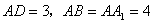 ,M是
,M是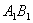 的中点.
的中点.
(1)求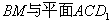 所成的角;
所成的角;
(2)求点M到平面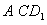 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com