
已知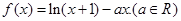
Ⅰ.求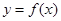 的单调区间;
的单调区间;
Ⅱ.当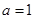 时,求
时,求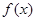 在定义域上的最大值;
在定义域上的最大值;
(Ⅰ)①当a = 0时,  的单调递增区间为
的单调递增区间为
②当a < 0 时,  的单调递增区间为
的单调递增区间为
③当a > 0时,  的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 。
。
(Ⅱ) 的最大值是0
的最大值是0
【解析】(I)先确定函数f(x)的定义域,然后再利用导数大(小)于零,分别求出其单调增区间或减区间.
(II)当a=1时,在(I)的基础上可知其单调性,进而可求出其最值.
解:(Ⅰ)定义域为 ,
, ———————————
———————————
①当a = 0时,
 ,
,
 的单调递增区间为
的单调递增区间为 —
—
②当a < 0 时,
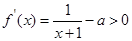

 的单调递增区间为
的单调递增区间为
③当a > 0时,由 ,则
,则 ,所以
,所以 的单调递增区间为
的单调递增区间为 ,
,
由 ,则
,则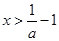 ,所以
,所以 的单调递减区间为
的单调递减区间为
(Ⅱ)当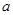 = 1时,
= 1时, ,
,
由(Ⅰ)可知 在
在 上单调递增,在
上单调递增,在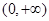 上单调递减,所以
上单调递减,所以
 的最大值是0
的最大值是0


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 7 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| c |
| d |
| a |
| b |
| c |
| a |
| b |
| d |
| a |
| b |
| a |
| b |
| c |
| d |
查看答案和解析>>
科目:高中数学 来源:2013年高考数学复习卷D(六)(解析版) 题型:解答题
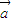 ,
, ,
,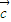 ,
, 及实数x,y且|
及实数x,y且|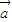 |=|
|=| |=1,
|=1, =
= +(x2-3)x
+(x2-3)x ,
,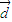 =-y
=-y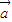 +
+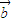 ,
,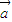 ⊥
⊥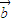 ,
, ⊥
⊥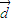 .
.查看答案和解析>>
科目:高中数学 来源:2010-2011学年甘肃省兰州一中高三(上)9月月考数学试卷(理科)(解析版) 题型:解答题
 (m<0),直线l与函数f(x),g(x)的图象都相切,且与函数f(x)的图象的切点横坐标为1.
(m<0),直线l与函数f(x),g(x)的图象都相切,且与函数f(x)的图象的切点横坐标为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com