
【题目】已知函数![]() .
.
(1)求函数![]() 的图像在
的图像在![]() 处的切线方程与
处的切线方程与![]() 的单调区间;
的单调区间;
(2)设![]() 是函数
是函数![]() 的导函数,试比较
的导函数,试比较![]() 与
与![]() 的大小.
的大小.
【答案】(1)![]() 函数的单调递增区间为
函数的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)![]() .
.
【解析】
(1)求![]() ,从而求得切线的斜率
,从而求得切线的斜率![]() ,即可求得切线方程,令
,即可求得切线方程,令![]() 及
及![]() ,分别求得函数
,分别求得函数![]() 的增、减区间。
的增、减区间。
(2)把![]() 与
与![]() 的大小问题转化成:
的大小问题转化成:![]() 与
与![]() 的大小问题来解决,令
的大小问题来解决,令![]() ,利用导数求出该函数的单调性,从而求出该函数的最大值,即可判断两个数的大小。
,利用导数求出该函数的单调性,从而求出该函数的最大值,即可判断两个数的大小。
解:(1)∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,所以所求切线方程为
,所以所求切线方程为![]() ,
,
即![]() .
.
令![]() ,解得
,解得![]() ,
,![]() ,解得
,解得![]() ,
,
所以函数的单调递增区间为![]() ,单调递减区间为
,单调递减区间为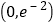 .
.
(2)∵![]() ,
,
∴![]() 与
与![]() 的大小关系等价于
的大小关系等价于![]() 与
与![]() 的大小关系,
的大小关系,
令![]() ,则
,则![]() ,
,
∵![]() 在
在![]() 上单调递减,且有
上单调递减,且有![]() ,
,![]() ,
,
∴![]() ,使
,使![]() ,即有
,即有![]() ,
,
即当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
即![]() ,
,
又由![]() ,可得
,可得![]() ,
,![]() ,
,
![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某通信公司为了配合客户的不同需要,现设计A,B两种优惠方案,这两种方案的应付话费y(元)与通话时间x(分钟)之间的关系如图所示(实线部分).(注:图中MN∥CD)
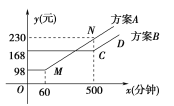
(1)若通话时间为2小时,则按方案A,B各付话费多少元?
(2)方案B从500分钟以后,每分钟收费多少元?
(3)通话时间在什么范围内,方案B才会比方案A优惠?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有编号为1,2,3,…,100的100把锁,利用中国剩余定理的原理设置开锁密码,规则为:将锁的编号依次除以3,5,7所得的三个余数作为该锁的开锁密码,这样,每把锁都有一个三位数字的开锁密码.例如,编号为52的锁所对应的开锁密码是123,开锁密码为232所对应的锁的编号是23.若一把锁的开锁密码为203,则这把锁的编号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月22日,国新办发布消息:新型冠状病毒来源于武汉一家海鲜市场非法销售的野生动.专家通过全基因组比对发现此病毒与2003年的非典冠状病毒以及此后的中东呼吸综合征冠状病毒,分别达到70%和40%的序列相似性.这种新型冠状病毒对人们的健康生命带来了严重威胁因此,某生物疫苗研究所加紧对新型冠状病毒疫苗进行实验,并将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如下:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
总计 | 50 | 50 | 100 |
现从所有试验小白鼠中任取一只,取到“注射疫苗”小白鼠的概率为![]() .
.
(1)求![]() 列联表中的数据
列联表中的数据![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)能否有99.9%把握认为注射此种疫苗对预防新型冠状病毒有效?
附:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
为了了解高中新生的体能情况,某学校抽取部分高一学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从 左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12﹒
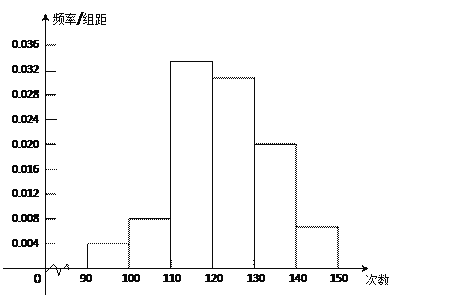
[来
(Ⅰ)第二小组的频率是多少?样本容量是多少?
(Ⅱ)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
(Ⅲ)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 垂直于直角梯形
垂直于直角梯形![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() .
.
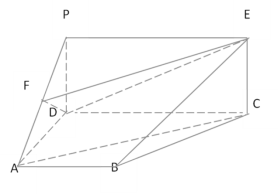
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ?若存在,请求出
?若存在,请求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=![]() x2+10x(万元).当年产量不小于80千件时,C(x)=51x+
x2+10x(万元).当年产量不小于80千件时,C(x)=51x+![]() -1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年开始,直播答题突然就火了,在某场活动中,最终仅有23人平分100万奖金,这23人可以说是“学霸”级的大神.但随着直播答题的发展,其模式的可持续性受到了质疑,某网战随机选取500名网民进行了调查,得到的数据如下表:
男 | 女 | |
认为直播答题模式可持续 | 180 | 140 |
认为直播答题模式不可持续 | 120 | 60 |
(1)根据表格中的数据,用独立性检验的思维方法判断是否有97.5%的把握认为对直播答题模式的态度与性别有关系?
(2)已知在参与调查的500人中,有15%曾参加答题游戏瓜分过奖金,而男性被调查者有12%曾参加游戏瓜分过奖金,求女性被调查者参与游戏瓜分过奖金的概率.
参考公式:![]()
临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com