
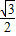 的椭圆
的椭圆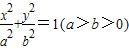 上的点到左焦点F的最长距离为
上的点到左焦点F的最长距离为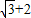 .
.
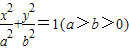 离心率为
离心率为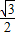 ,其上的点到左焦点F的最长距离为
,其上的点到左焦点F的最长距离为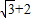 ,可建立方程组,即可求得椭圆的方程;
,可建立方程组,即可求得椭圆的方程;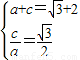 ,∴a=2,c=
,∴a=2,c=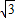 ,∴
,∴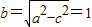
 ;
;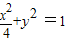 的左特征点,椭圆的左焦点F(-
的左特征点,椭圆的左焦点F(-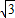 ,0),
,0),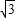 (k≠0)
(k≠0)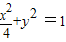 ,得:(ky-
,得:(ky-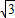 )y2+4y2=4,即(k2+4)y2-
)y2+4y2=4,即(k2+4)y2-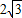 ky-1=0,
ky-1=0,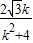 ,y1y2=-
,y1y2=-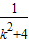
 ,
,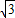 )+y2(ky1-
)+y2(ky1-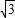 )-(y1+y2)m=0
)-(y1+y2)m=0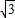 )=0
)=0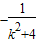 )-
)-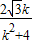 ×(m+
×(m+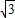 )=0
)=0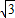 (m+
(m+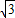 )=0,即m=
)=0,即m=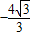 ,∴M(
,∴M(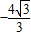 ,0)
,0)

 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源:2012-2013学年广西柳铁一中高三下学期模拟考试(二)文科数学试卷(解析版) 题型:解答题
已知离心率为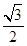 的椭圆
的椭圆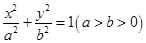 上的点到左焦点
上的点到左焦点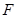 的最长距离为
的最长距离为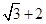 .
.
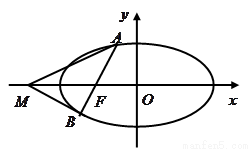
(Ⅰ)求椭圆的方程;
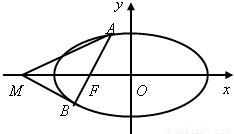
(Ⅱ)如图,过椭圆的左焦点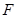 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦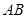 ,若点
,若点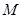 在
在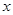 轴上,且使得
轴上,且使得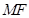 为
为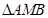 的一条内角平分线,则称点
的一条内角平分线,则称点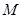 为该椭圆的“左特征点”,求椭圆的“左特征点”
为该椭圆的“左特征点”,求椭圆的“左特征点”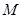 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广西桂林十八中高三第二次月考试卷理科数学 题型:解答题
(本小题满分12分)已知离心率为 的椭圆
的椭圆 上的点到
上的点到
左焦点 的最长距离为
的最长距离为
(1)求椭圆的方程;
(2)如图,过椭圆的左焦点 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦 ,若点
,若点 在
在 轴上,且使得
轴上,且使得 为
为 的一条内角平分线,则称点
的一条内角平分线,则称点 为该椭圆的“左特征点”,求椭圆的“左特征点”
为该椭圆的“左特征点”,求椭圆的“左特征点” 的坐标.
的坐标.

查看答案和解析>>
科目:高中数学 来源:广西桂林十八中2011-2012学年高三第二次月考试题数学文 题型:解答题
已知离心率为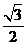 的椭圆
的椭圆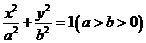 上的点到左焦点
上的点到左焦点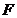 的最长距离为
的最长距离为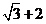 .
.
(1)求椭圆的方程;
(2)如图,过椭圆的左焦点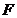 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦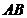 ,若点
,若点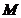 在
在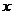 轴上,且使得
轴上,且使得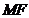 为
为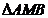 的一条内角平分线,则称点
的一条内角平分线,则称点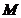 为该椭圆的“左特征点”,求椭圆的“左特征点”
为该椭圆的“左特征点”,求椭圆的“左特征点”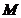 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源:广西桂林十八中2011-2012学年高三第二次月考试题数学理 题型:解答题
已知离心率为 的椭圆
的椭圆 上的点到左焦点
上的点到左焦点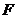 的最长距离为
的最长距离为
(1)求椭圆的方程;
(2)如图,过椭圆的左焦点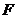 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦 ,若点
,若点 在
在 轴上,且使得
轴上,且使得 为
为 的一条内角平分线,则称点
的一条内角平分线,则称点 为该椭圆的“左特征点”,求椭圆的“左特征点”
为该椭圆的“左特征点”,求椭圆的“左特征点” 的坐标.
的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com