
【题目】已知![]() ,记
,记![]() 为正整数a的各位数字之和。试求正整数t的最小值,使得在任意t个连续的正整数中总能找到一个数c,满足
为正整数a的各位数字之和。试求正整数t的最小值,使得在任意t个连续的正整数中总能找到一个数c,满足![]() 。
。
【答案】见解析
【解析】
设![]() .则
.则
当10![]() (a+1)时,f(a+1)=f(a)+1;
(a+1)时,f(a+1)=f(a)+1;
当![]() 时,
时,
![]() .
.
首先证明:在任意![]() 个连续正整数中,总能找到一个数c,满足m|f(c).
个连续正整数中,总能找到一个数c,满足m|f(c).
若这t个数中有![]() 的倍数,设其为
的倍数,设其为![]() .
.
则f(a)=f(b)=s.
由![]() ,其中,u=0,1,...,8;v=0,1,...,k,知
,其中,u=0,1,...,8;v=0,1,...,k,知![]() 的f值为
的f值为
![]() ,
,
其中,必有一个为9k+r的倍数.
由![]() ,其中,u=0,1,...,9;u=0,1,...,k,知
,其中,u=0,1,...,9;u=0,1,...,k,知![]() 的f值为
的f值为
![]() ,
,
其中,必有一个为9k+r的倍数.
若这t个数中没有![]() 的倍数,则其中有
的倍数,则其中有![]() 的倍数.设最小的倍数为a,f(a)=s.
的倍数.设最小的倍数为a,f(a)=s.
同上,知![]() 的f值为
的f值为![]() ,其中,必有一个为9k+r的倍数.
,其中,必有一个为9k+r的倍数.
综上,在![]() 个连续正整数中必有一数c,满足m|f(c).
个连续正整数中必有一数c,满足m|f(c).
从而,![]() .
.
其次,分三种情形求![]() .
.
1 当r=1,2,4,5,7,8时,![]() .
.
下面构造![]() 个连续正整数,使得其中没有数c,满足mlf(c).
个连续正整数,使得其中没有数c,满足mlf(c).
取![]() ,满足(9k+r)|(9i+1).则在
,满足(9k+r)|(9i+1).则在![]() 中,只有首尾两数的f值是9k+r的倍数.故中间的
中,只有首尾两数的f值是9k+r的倍数.故中间的![]() 个连续正整数中没有数c,满足(9k+r)|f(c).
个连续正整数中没有数c,满足(9k+r)|f(c).
2 当r=3,6时,![]() .
.
因![]() 个连续正整数中必有一数c,满足(9k+r)|f(c).此时,3|f(c).而
个连续正整数中必有一数c,满足(9k+r)|f(c).此时,3|f(c).而![]() 的末尾三数中各自只有一个数是3的倍数,故在连续
的末尾三数中各自只有一个数是3的倍数,故在连续![]() 个数A中首尾共
个数A中首尾共![]() 个数可以去掉,即在
个数可以去掉,即在![]() 个连续正整数中必有一数c,满足(9h+r)|f(c).
个连续正整数中必有一数c,满足(9h+r)|f(c).
下面构造![]() 个连续正整数,使得其中没有数c,满足m|f(c).
个连续正整数,使得其中没有数c,满足m|f(c).
取![]() ,满足(9k+r)|(9i+3),则在
,满足(9k+r)|(9i+3),则在![]() 至
至![]() 这
这![]() 个连续正整数中没有数c,满足(9k+r)|f(c).
个连续正整数中没有数c,满足(9k+r)|f(c).
3 当r=9时,![]() .
.
类似(2)知,9|f(c)且![]() 的末尾九个数中各自只有一个数是9的倍数.
的末尾九个数中各自只有一个数是9的倍数.
故在![]() 个连续正整数中必有一数c,满足9(k+1)|f(c),且在
个连续正整数中必有一数c,满足9(k+1)|f(c),且在
![]() 至
至![]() 这
这![]() 个连续正整数中没有数c,满足9(k+1)|f(c).
个连续正整数中没有数c,满足9(k+1)|f(c).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
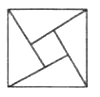
【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形,若直角三角形的直角边的边长分别是3和4,在绘图内随机取一点,则此点取自小正方形的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有9名学生在同一间教室参加一次数学竞赛,座位排列成3行3列,用![]() 的方格棋盘表示,其中,每个方格代表一个座位为了避免舞弊,采用A、B、C三种类型的试卷,要使任何两个相邻的座位(有公共边的两个方格)发放的试卷类型不同.则符合条件的发放试卷的方法共有________种.
的方格棋盘表示,其中,每个方格代表一个座位为了避免舞弊,采用A、B、C三种类型的试卷,要使任何两个相邻的座位(有公共边的两个方格)发放的试卷类型不同.则符合条件的发放试卷的方法共有________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为![]() 的菱形
的菱形![]() 中,
中,![]() .点
.点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,点
上,点![]() 与点
与点![]() ,
,![]() 不重合,
不重合,![]() ,
,![]() .沿
.沿![]() 将
将![]() 翻折到
翻折到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)当![]() 与平面
与平面![]() 所成的角为
所成的角为![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为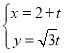 (
(![]() 为参数),
为参数),![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,设
两点,设![]() 、
、![]() 中点为
中点为![]() ,求弦长
,求弦长![]() 以及
以及![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,再随机抽取3人赠送礼品,记这3人中“微信控”的人数为![]() ,试求
,试求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com