
(2009湖南卷理)(本小题满分12分)
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的.![]() 、
、![]() 、
、![]() ,现在3名工人独立地从中任选一个项目参与建设。
,现在3名工人独立地从中任选一个项目参与建设。 ![]()
![]()
(I)求他们选择的项目所属类别互不相同的概率;
(II)记![]() 为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求
为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求![]() 的分布列及数学期望。
的分布列及数学期望。
解析:记第1名工人选择的项目属于基础设施工程、民生工程和产业建设工程分别为事件 ![]() ,
,![]() ,
,![]() ,i=1,2,3.由题意知
,i=1,2,3.由题意知![]()
![]() 相互独立,
相互独立,![]()
![]() 相互独立,
相互独立,![]()
![]() 相互独立,
相互独立,![]() ,
,![]() ,
,![]() (i,j,k=1,2,3,且i,j,k互不相同)相互独立,且P(
(i,j,k=1,2,3,且i,j,k互不相同)相互独立,且P(![]() )=,P(
)=,P(![]() )=
)=![]() ,P(
,P(![]() )=
)=![]()
(1) 他们选择的项目所属类别互不相同的概率
P=3!P(![]()
![]()
![]() )=6P(
)=6P(![]() )P(
)P(![]() )P(
)P(![]() )=6
)=6![]()
![]()
![]()
![]()
![]()
![]() =
=![]()
(2) 解法1 设3名工人中选择的项目属于民生工程的人数为![]() ,由己已知,
,由己已知,![]() -B(3,
-B(3,![]() ),且
),且![]() =3
=3![]() 。
。
所以P(![]() =0)=P(
=0)=P(![]() =3)=
=3)=![]()
![]() =
=![]() ,
,
P(![]() =1)=P(
=1)=P(![]() =2)=
=2)= ![]()
![]()
![]() =
= ![]()
![]()
![]()
P(![]() =2)=P(
=2)=P(![]() =1)=
=1)=![]()
![]()
![]() =
=![]()
P(![]() =3)=P(
=3)=P(![]() =0)=
=0)= ![]()
![]() =
= ![]()
故![]() 的分布是
的分布是
| 0 | 1 | 2 | 3 |
P |
|
|
|
|
![]() 的数学期望E
的数学期望E![]() =0
=0![]()
![]() +1
+1![]()
![]() +2
+2![]()
![]() +3
+3![]()
![]() =2
=2
解法2 第i名工人选择的项目属于基础工程或产业工程分别为事件![]() ,
,
i=1,2,3 ,由此已知,![]() ?D,
?D,![]() 相互独立,且
相互独立,且
P(![]() )-(
)-(![]() ,
,![]() )= P(
)= P(![]() )+P(
)+P(![]() )=
)=![]() +
+![]() =
=![]()
所以![]() --
--![]() ,既
,既![]() ,
,![]()
![]()
![]()
故![]() 的分布列是
的分布列是
|
| 1 | 2 | 3 |
|
|
|
|
|


科目:高中数学 来源: 题型:
(2009湖南卷理)从10名大学生毕业生中选3个人担任村长助理,则甲、乙至少有1人入选,而丙没有入选的不同选法的种数位 ![]()
![]() [ ]
[ ]
A 85 B
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009湖南卷理)设函数![]() 在(
在(![]() ,+
,+![]() )内有定义。对于给定的正数K,定义函数
)内有定义。对于给定的正数K,定义函数
![]()
取函数![]() =
=![]() 。若对任意的
。若对任意的![]() ,恒有
,恒有![]() =
=![]() ,则
,则 ![]()
![]()
A.K的最大值为2 B. K的最小值为2
C.K的最大值为1 D. K的最小值为1 【 】
查看答案和解析>>
科目:高中数学 来源: 题型:
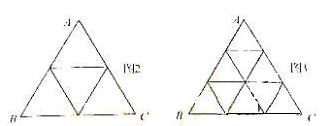
(2009湖南卷理)将正ABC分割成![]()
![]() (
(![]() ≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)= ,…,
≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)= ,…,

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com