
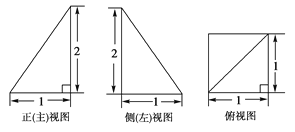
【题目】已知四棱锥P-ABCD的三视图如下图所示,E是侧棱PC上的动点.
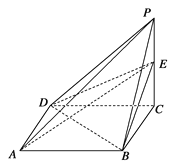
(1)求证:BD⊥AE
(2)若点E为PC的中点,求二面角D-AE-B的大小.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)要证明线线垂直,先证明线面垂直,所以观察几何体,先证明![]() 平面
平面![]() ,而要证明线面垂直,先证明线与平面内的两条相交直线垂直,即证明
,而要证明线面垂直,先证明线与平面内的两条相交直线垂直,即证明![]() ,
,![]() ;
;
(2)法一,几何法,观察![]() ,所以可选择在平面DAE内过点D作DF⊥AE于F,连结BF,∠DFB为二面角D-AE-B的平面角,或法二,采用空间向量的方法,以点C为原点,CD,CB,CP所在的直线分别为x,y,z轴建立空间直角坐标系,分别求两个平面的法向量,
,所以可选择在平面DAE内过点D作DF⊥AE于F,连结BF,∠DFB为二面角D-AE-B的平面角,或法二,采用空间向量的方法,以点C为原点,CD,CB,CP所在的直线分别为x,y,z轴建立空间直角坐标系,分别求两个平面的法向量,![]() 或
或![]() .
.
试题解析:(1)由三视图可知,四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC=2.
连结AC,∵ABCD是正方形, ∴BD⊥AC.
∵PC⊥底面ABCD,且BD平面ABCD, ∴BD⊥PC.
又∵AC∩PC=C,∴BD⊥平面PAC.
∵AE平面PAC. ∴BD⊥AE.
(2)解法1:在平面DAE内过点D作DF⊥AE于F,连结BF.
∵AD=AB=1,DE=BE=![]() ,AE=AE=
,AE=AE=![]() ,
,
∴Rt△ADE≌Rt△ABE,
从而△ADF≌△ABF,∴BF⊥AE.
∴∠DFB为二面角D-AE-B的平面角.
在Rt△ADE中,DF=![]() , ∴
, ∴![]() .
.
又BD=![]() ,在△DFB中,由余弦定理得
,在△DFB中,由余弦定理得
cos∠DFB=![]() ,
,
∴∠DFB=![]() ,即二面角D-AE-B的大小为
,即二面角D-AE-B的大小为![]()
解法2:如图,以点C为原点,CD,CB,CP所在的直线分别为x,y,z轴建立空间直角坐标系.则D(1,0,0),A(1,1,0),B(0,1,0),E(0,0,1),
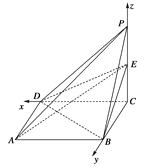
从而![]() =(0,1,0),
=(0,1,0),![]() =(-1,0,1),
=(-1,0,1),![]() =(1,0,0),
=(1,0,0),![]() =(0,-1,1).[Z#x设平面ADE和平面ABE的法向量分别为
=(0,-1,1).[Z#x设平面ADE和平面ABE的法向量分别为![]() ,
,![]()
由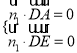
![]() ,取
,取![]()
由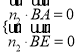
![]() ,取
,取![]()
设二面角D-AE-B的平面角为θ,则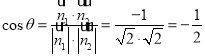 ,
,
∴θ=![]() ,即二面角D-AE-B的大小为
,即二面角D-AE-B的大小为![]()


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均为正数,前
的各项均为正数,前![]() 项和
项和![]() 满足
满足![]() ;数列
;数列![]() 是等比数列,前
是等比数列,前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知等比数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,求数列
,求数列![]() 前
前![]() 项和为
项和为![]() ;
;
(3)若![]() ,且等比数列
,且等比数列![]() 的公比
的公比![]() ,若存在
,若存在![]() ,使得
,使得![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,过焦点且与
,过焦点且与![]() 轴垂直的直线被椭圆
轴垂直的直线被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知点![]() ,
,![]() ,过点
,过点![]() 的任意一条直线
的任意一条直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域是一切实数的函数![]() ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数![]() 使得
使得![]() 对任意实数
对任意实数![]() 都成立,则称
都成立,则称![]() 是一个“
是一个“![]() —伴随函数”.有下列关于—伴随函数”的结论:
—伴随函数”.有下列关于—伴随函数”的结论:
①![]() 是常数函数中唯一一个“
是常数函数中唯一一个“![]() —伴随函数”;②“
—伴随函数”;②“![]() —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;
③![]() 是一个—伴随函数”;其中正确的是( )
是一个—伴随函数”;其中正确的是( )
A.①B.②C.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的右焦点为F(1,0),且点P
(a>b>0)的右焦点为F(1,0),且点P![]() 在椭圆C上,O为坐标原点.
在椭圆C上,O为坐标原点.
(1)求椭圆C的标准方程;
(2)设过定点T(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】赵爽是我国古代数学家、天文学家大约在公元222年赵爽为《周碑算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的)类比“赵爽弦图”,赵爽弦图可类似地构造如图所示的图形,它是由个3全等的等边三角形与中间的一个小等边三角形组成的一个大等边三角形,设DF2AF,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是( )
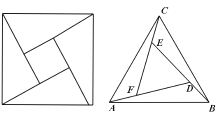
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com