
已知三棱柱 的侧棱长和底面边长均为2,
的侧棱长和底面边长均为2, 在底面ABC内的射影O为底面△ABC的中心,如图所示:
在底面ABC内的射影O为底面△ABC的中心,如图所示:

(1)联结 ,求异面直线
,求异面直线 与
与 所成角的大小;
所成角的大小;
(2)联结 、
、 ,求三棱锥C1-BCA1的体积.
,求三棱锥C1-BCA1的体积.
(1)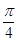 ;(2)
;(2)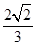 .
.
【解析】
试题分析:(1)要求异面直线所成的角,必须按照定义作出这个角,即把异面直线平移为相交直线,求相交直线所夹的锐角或直角,当然我们一般是过异面直线中的某一条上一点作另一条直线的平行线,同时要借助已知图形中的平行关系寻找平行线,以方便解题.本题是三棱柱,显然有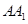 ∥
∥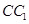 ,因此只要在
,因此只要在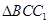 中求
中求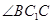 即可;(2)求三棱锥的体积,一般用公式
即可;(2)求三棱锥的体积,一般用公式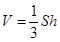 ,即底面面积乘以高再除以3,但本题中由于三棱锥的高不容易找,而这个三棱锥在三棱柱中,因此我们可借助三棱柱来求棱锥的体积,利用棱锥体积的公式,可知这个三棱柱被分成三个体积相等的三棱锥
,即底面面积乘以高再除以3,但本题中由于三棱锥的高不容易找,而这个三棱锥在三棱柱中,因此我们可借助三棱柱来求棱锥的体积,利用棱锥体积的公式,可知这个三棱柱被分成三个体积相等的三棱锥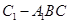 ,
,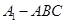 ,
,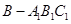 ,因此我们只要求三棱柱的体积即可.
,因此我们只要求三棱柱的体积即可.
试题解析:(1) 联结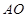 ,并延长与
,并延长与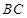 交于点
交于点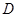 ,则
,则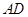 是
是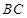 边上的中线.
边上的中线.
 点
点 是正
是正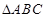 的中心,且
的中心,且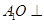 平面
平面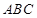 ,
,
∴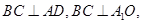 且
且 .∴
.∴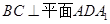 .
.
∴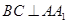 .
.
又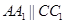 ,
,
∴异面直线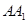 与
与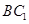 所成的角为
所成的角为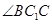 .
.
∴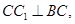 即四边形
即四边形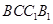 为正方形.
为正方形.
∴异面直线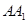 与
与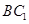 所成角的大小为
所成角的大小为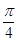 .
.
(2)∵三棱柱的所有棱长都为2,
∴可求算得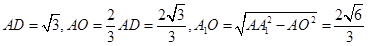 .
.
∴ ,
,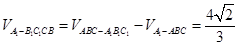 .
.
∴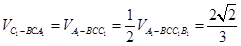 .
.
考点:(1)异面直线所成的角;(2)三棱锥的体积.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
(1)求异面直线AC与BC1所成角的余弦值;
(2)求证:A1B⊥面AB1C.
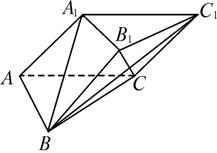
查看答案和解析>>
科目:高中数学 来源: 题型:
(12分)如图所示,已知三棱柱ABC-![]() 的底面边长均为2,侧棱
的底面边长均为2,侧棱![]() 的长为2且与底面ABC所成角为
的长为2且与底面ABC所成角为![]() ,且侧面
,且侧面![]() 垂直于底面ABC.
垂直于底面ABC.
(1)求二面角![]() 的正切值的大小;
的正切值的大小;
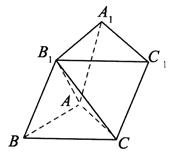 (2)若其余条件不变,只改变侧棱的长度,当侧棱
(2)若其余条件不变,只改变侧棱的长度,当侧棱![]() 的长度为多长时,可使面
的长度为多长时,可使面![]() 和底面垂直.
和底面垂直.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海黄浦区高三上学期期末考试(即一模)文数学卷(解析版) 题型:解答题
已知三棱柱 的侧棱长和底面边长均为2,
的侧棱长和底面边长均为2, 在底面ABC内的射影O为底面△ABC的中心,如图所示:
在底面ABC内的射影O为底面△ABC的中心,如图所示:

(1)联结 ,求异面直线
,求异面直线 与
与 所成角的大小;
所成角的大小;
(2)联结 、
、 ,求四棱锥
,求四棱锥 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com