
(Ⅰ)证明:![]() <lgSn+1;
<lgSn+1;
(Ⅱ)是否存在常数C>0使得![]() =lg(Sn+1-C)成立?并证明你的结论.
=lg(Sn+1-C)成立?并证明你的结论.
| (Ⅰ)证明:设{an}的公比为q,由题设知a1>0,q>0
(ⅰ)当q=1时,Sn=a1n,从而 SnSn+2-Sn+12=a1n(n+2)a1-(n+1)2a12=-a12<0 (ⅱ)当q≠1时,Sn= SnSn+2-Sn+12= 由(ⅰ)和(ⅱ)得SnSn+2<Sn+12 根据对数函数的单调性知lg(SnSn+2)<lgSn+12 即 (Ⅱ)解:不存在. 证法一:要使
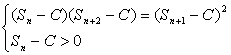
分两种情况讨论: (ⅰ)当q=1时, (Sn-C)(Sn+2-C)-(Sn+1-C)2= (a1n-C)[a1(n+2)-C]-[a1(n+1)-C]2 =-a12<0 可知,不满足条件①,即不存在常数C>0,使结论成立. (ⅱ)当q≠1时, (Sn-C)(Sn+2-C)-(Sn+1-C)2
因a1qn≠0,若条件①成立,故只能是a1-C(1-q)=0,即C= 综合(ⅰ)、(ⅱ),同时满足条件①,②的常数C>0不存在,即不存在常数C>0, 使 证法二:用反证法,假设存在常数C>0,使

由④得SnSn+2-Sn+12=C(Sn+Sn+2-2Sn+1 ⑤ 根据平均值不等式及①、②、③、④知 Sn+Sn+2-2Sn+1=(Sn-C)+(Sn+2-C)-2(Sn+1-C) ≥ 因为C>0,故⑤式右端非负,而由(Ⅰ)知,⑤式左端小于零,矛盾, 故不存在常数C<0,使
|


科目:高中数学 来源:2011届湖北省夷陵中学、钟祥一中高三第二次联考数学理卷 题型:解答题
(12分)设{an}是由正数组成的等差数列,Sn是其前n项和
(1)若Sn=20,S2n=40,求S3n的值;
(2)若互不相等正整数p,q,m,使得p+q=2m,证明:不等式SpSq<S 成立;
成立;
(3)是否存在常数k和等差数列{an},使ka -1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
-1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2014届广东省高一6月月考数学试卷(解析版) 题型:选择题
设{an}是由正数组成的等比数列,且a5a6=81,log3a1+ log3a2+…+ log3a10的值是( )
A.5 B.10; C.20 D.2或4
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三11月月考理科数学试卷 题型:解答题
(本题满分14分) 设{an}是由正数组成的等差数列,Sn是其前n项和
(1)若 ,求
,求 的值;
的值;
(2)若互不相等正整数p,q,m,使得p+q=2m,证明:不等式 成立;
成立;
(3)是否存在常数k和等差数列{an},使 恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省、钟祥一中高三第二次联考数学理卷 题型:解答题
(12分)设{an}是由正数组成的等差数列,Sn是其前n项和
(1)若Sn=20,S2n=40,求S3n的值;
(2)若互不相等正整数p,q,m,使得p+q=2m,证明:不等式SpSq<S 成立;
成立;
(3)是否存在常数k和等差数列{an},使ka -1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
-1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省、钟祥一中高三第二次联考数学理卷 题型:解答题
(12分)设{an}是由正数组成的等差数列,Sn是其前n项和
(1)若Sn=20,S2n=40,求S3n的值;
(2)若互不相等正整数p,q,m,使得p+q=2m,证明:不等式SpSq<S 成立;
成立;
(3)是否存在常数k和等差数列{an},使ka -1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
-1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com