分析:①当 当a>1时,方程2x-log
ax=0 无解,故①不正确.
②(x-2)•
≥0的解集为[2,+∞)∪{1},故②不正确.
③由“x<1”能推出“x<2”; 但由“x<2”,不能推出“x<1”,故③正确.
④函数y=x
3过点A (1,1)的切线的斜率为3,切线方程为 y-1=3(x-1),故④正确.
⑤如图:由条件可得BC为直径,三角形AOB为等边三角形,向量
在向量
方向上的投影为1×cos60°=
,
故⑤正确.
解答:解:①当 0<a<1时,方程2x-log
ax=0的解有1个; 当a>1时,方程2x-log
ax=0 无解,故①不正确.
②(x-2)•
≥0的解集为[2,+∞)∪{1},故②不正确.
③由“x<1”能推出“x<2”; 但由“x<2”,不能推出“x<1”(如x=1.5),
故“x<1”是“x<2”的充分不必要条件,故③正确.
④函数y=x
3过点A (1,1)的切线的斜率为3,切线方程为 y-1=3(x-1),即 y=3x-2,故④正确.
⑤如图:△ABC的外接圆的圆心为0,半径为1,
+
=2
,且|
|=|
|,∴O为BC的中点,
BC为直径,三角形AOB为等边三角形,则向量
在向量
方向上的投影为1×cos60°=
,故⑤正确.
故答案为:③④⑤.
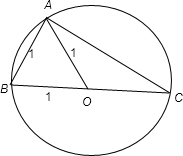
⑤
点评:本题考查不等式与不等关系,充分条件、必要条件的定义,利用导数求切线的斜率,一个向量在另一个向量上
的投影的意义,画出图形是解题的关键,属于基础题.

 ⑤
⑤

![]() )、N(-4,
)、N(-4,![]() ),给出下列曲线方程:①2x+y-1=0;②2x-4y+3=0;③x2+y2=3;④(x+3)2+y2=1.
),给出下列曲线方程:①2x+y-1=0;②2x-4y+3=0;③x2+y2=3;④(x+3)2+y2=1.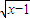 ≥0的解集为[2,+∞).
≥0的解集为[2,+∞).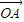 +
+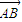 +
+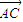 =
=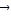 ,且|
,且|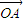 |=|
|=|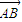 |
|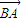 在向量
在向量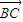 方向上的投影为
方向上的投影为 .其中真命题的序号是 (写出所有正确命题的编号).
.其中真命题的序号是 (写出所有正确命题的编号).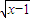 ≥0的解集为[2,+∞)
≥0的解集为[2,+∞)