
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为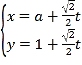 (
(![]() 为参数,
为参数,![]() ).以
).以![]() 为极点,
为极点,![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在平行四边形ABCD中,AB=1,AD![]() ,且∠BAD=45°,以BD为折线,把△ABD折起,使AB⊥DC,连接AC,得到三棱锥A﹣BCD.
,且∠BAD=45°,以BD为折线,把△ABD折起,使AB⊥DC,连接AC,得到三棱锥A﹣BCD.
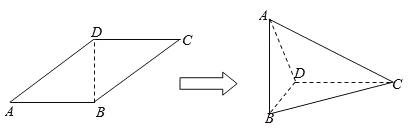
(1)求证:平面ABD⊥平面BCD;
(2)求二面角B﹣AC﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正实数列a1,a2,…满足对于每个正整数k,均有![]() ,证明:
,证明:
(Ⅰ)a1+a2≥2;
(Ⅱ)对于每个正整数n≥2,均有a1+a2+…+an≥n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为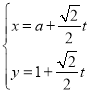 (
(![]() 为参数,
为参数,![]() ).以
).以![]() 为极点,
为极点,![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°.PA⊥面ABCD,且PA=3.F在棱PA上,且AF=1,E在棱PD上.
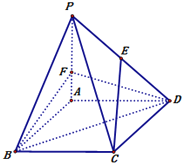
(Ⅰ)若CE∥面BDF,求PE:ED的值;
(Ⅱ)求二面角B-DF-A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“工资条里显红利,个税新政入民心”.随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.某![]() 从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁-35岁(2009年-2018年)之间各年的月平均收入
从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁-35岁(2009年-2018年)之间各年的月平均收入![]() (单位:千元)的散点图:(注:年龄代码1-10分别对应年龄26-35岁)
(单位:千元)的散点图:(注:年龄代码1-10分别对应年龄26-35岁)
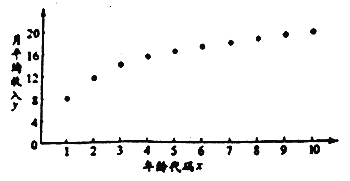
(1)由散点图知,可用回归模型![]() 拟合
拟合![]() 与
与![]() 的关系,试根据有关数据建立
的关系,试根据有关数据建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)如果该![]() 从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入视为月收入,根据新旧个税政策,估计他36岁时每个月少缴纳的个人所得税.
从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入视为月收入,根据新旧个税政策,估计他36岁时每个月少缴纳的个人所得税.
附注:①参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,其中
,其中![]() :取
:取![]() ,
,![]() .
.
②参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为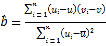 ,
,![]() .
.
③新旧个税政策下每月应纳税所得额(含税)计算方法及税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
缴税 级数 | 每月应纳税所得额(含税) | 税率 | 每月应纳税所得额(含税) | 税率 |
1 | 不超过1500元的都分 | 3 | 不超过3000元的都分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元的部分 | 30 | 超过35000元至55000元的部分 | 30 |
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某市高三数学复习备考情况,该市教研机构组织了一次检测考试,并随机抽取了部分高三理科学生数学成绩绘制如图所示的频率分布直方图.

(1)根据频率分布直方图,估计该市此次检测理科数学的平均成绩![]() ;(精确到个位)
;(精确到个位)
(2)研究发现,本次检测的理科数学成绩![]() 近似服从正态分布
近似服从正态分布![]() (
(![]() ,
,![]() 约为
约为![]() ),按以往的统计数据,理科数学成绩能达到自主招生分数要求的同学约占
),按以往的统计数据,理科数学成绩能达到自主招生分数要求的同学约占![]() .
.
(ⅰ)估计本次检测成绩达到自主招生分数要求的理科数学成绩大约是多少分?(精确到个位)
(ⅱ)从该市高三理科学生中随机抽取![]() 人,记理科数学成绩能达到自主招生分数要求的人数为
人,记理科数学成绩能达到自主招生分数要求的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .(说明:
.(说明:![]() 表示
表示![]() 的概率.参考数据:
的概率.参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com