
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asinB=﹣bsin(A+ ![]() ).
).
(1)求A;
(2)若△ABC的面积S= ![]() c2 , 求sinC的值.
c2 , 求sinC的值.
【答案】
(1)解:∵asinB=﹣bsin(A+ ![]() ).
).
∴由正弦定理可得:sinAsinB=﹣sinBsin(A+ ![]() ).即:sinA=﹣sin(A+
).即:sinA=﹣sin(A+ ![]() ).
).
可得:sinA=﹣ ![]() sinA﹣
sinA﹣ ![]() cosA,化简可得:tanA=﹣
cosA,化简可得:tanA=﹣ ![]() ,
,
∵A∈(0,π),
∴A= ![]()
(2)解:∵A= ![]() ,
,
∴sinA= ![]() ,
,
∵由S= ![]() c2=
c2= ![]() bcsinA=
bcsinA= ![]() bc,可得:b=
bc,可得:b= ![]() ,
,
∴a2=b2+c2﹣2bccosA=7c2,可得:a= ![]() ,
,
由正弦定理可得:sinC= ![]()
【解析】(1)由正弦定理化简已知可得tanA=﹣ ![]() ,结合范围A∈(0,π),即可计算求解A的值.(2)由(1)可求sinA=
,结合范围A∈(0,π),即可计算求解A的值.(2)由(1)可求sinA= ![]() ,利用三角形面积公式可求b=
,利用三角形面积公式可求b= ![]() ,利用余弦定理可求a=
,利用余弦定理可求a= ![]() ,由正弦定理即可计算求解.
,由正弦定理即可计算求解.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD= ![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°. 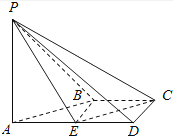
(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(2)若二面角P﹣CD﹣A的大小为45°,求直线PA与平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga![]() (a>0且a≠1)是奇函数,
(a>0且a≠1)是奇函数,
(1)求实数m的值;
(2)若a=![]() ,并且对区间[3,4]上的每一个x的值,不等式f(x)>(
,并且对区间[3,4]上的每一个x的值,不等式f(x)>(![]() )x+t恒成立,求实数t的取值范围.
)x+t恒成立,求实数t的取值范围.
(3)当x∈(r,a-2)时,函数f(x)的值域是(1,+∞),求实数a与r的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1) 把![]() 的图象上每一点的纵坐标变为原来的
的图象上每一点的纵坐标变为原来的![]() 倍,再将横坐标向右平移
倍,再将横坐标向右平移![]() 个单位,可得
个单位,可得![]() 图象,求
图象,求![]() ,
,![]() 的值;
的值;
(2) 若对任意实数![]() 和任意
和任意![]() ,恒有
,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1 , BC的中点. 
(1)证明:平面AEB⊥平面BB1C1C;
(2)证明:C1F∥平面ABE;
(3)设P是BE的中点,求三棱锥P﹣B1C1F的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】砂糖橘是柑橘类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植砂糖橘,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的![]() 倍.
倍.

(1)求a,b的值;
(2)从样本中产量在区间(50,60]上的果树里随机抽取两株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的奇函数f(x)的周期为4,且x∈(0,2)时f(x)=ln(x2﹣x+b),若函数f(x)在区间[﹣2,2]上恰有5个零点,则实数b应满足的条件是( )
A.﹣1<b≤1
B.﹣1<b<1或b= ![]()
C.![]() <b
<b ![]()
D.![]() <b≤1或b=
<b≤1或b= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙,丙三位学生独立地解同一道题,甲做对的概率为 ![]() ,乙,丙做对的概率分别为m,n(m>n),且三位学生是否做对相互独立.记ξ为这三位学生中做对该题的人数,其分布列为:
,乙,丙做对的概率分别为m,n(m>n),且三位学生是否做对相互独立.记ξ为这三位学生中做对该题的人数,其分布列为:
ξ | 0 | 1 | 2 | 3 |
P |
| a | b |
|
(1)求至少有一位学生做对该题的概率;
(2)求m,n的值;
(3)求ξ的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com