
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,其前9项和为63.
,其前9项和为63.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,若对任意正整数n,都有
,若对任意正整数n,都有![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1) an=n;bn=n+2.
(2) ![]() .
.
【解析】分析:(1)由题意结合所给条件可知数列![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列,据此计算可得
的等差数列,据此计算可得![]() ,利用递推关系式可得
,利用递推关系式可得![]() .
.
(2)由(1)裂项求和可得![]() ,据此整理计算可得
,据此整理计算可得![]() 的最小值为
的最小值为![]() .
.
详解:(1)由2nSn+1-2(n+1)Sn=n(n+1),得![]() -
-![]() =
=![]() ,
,
所以数列![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列,
的等差数列,
因此![]() =S1+(n-1)×
=S1+(n-1)×![]() =
=![]() n+
n+![]() ,即Sn=
,即Sn=![]() .
.
于是an+1=Sn+1-Sn=![]() -
-![]() =n+1,
=n+1,
所以an=n.
因为bn+2-2bn+1+bn=0,所以数列![]() 是等差数列,
是等差数列,
由{bn}的前9项和为63,得![]() =63,
=63,
又b3=5,所以b7=9,
所以数列{bn}的公差d=![]() =1,
=1,
则bn=b3+(n-3)×1=n+2.
(2)由(1)知cn=![]() +
+![]() =
=![]() +
+![]() =2+2(
=2+2(![]() -
-![]() ),
),
所以Tn=c1+c2+…+cn=2n+2(1-![]() +
+![]() -
-![]() +
+![]() -
-![]() +…+
+…+![]() -
-![]() +
+![]() -
-![]() )
)
=2n+2(1+![]() -
-![]() -
-![]() )=3-2(
)=3-2(![]() +
+![]() )+2n,
)+2n,
则Tn-2n=3-2(![]() +
+![]() ).
).
设An=Tn-2n=3-2(![]() +
+![]() ).
).
因为An+1-An=3-2(![]() +
+![]() )-[3-2(
)-[3-2(![]() +
+![]() )]=2(
)]=2(![]() -
-![]() )=
)=![]() >0,
>0,
所以数列{An}为递增数列,则(An)min=A1=![]() .
.
又因为An=3-2![]() <3,所以
<3,所以![]() ≤An<3.
≤An<3.
因为对任意正整数n,Tn-2n∈[a,b],所以a≤![]() ,b≥3,则(b-a)min=3-
,b≥3,则(b-a)min=3-![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】在△ABC中,a、b、c分别为内角A、B、C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC
(1)求A的大小;
(2)若sinB+sinC=1,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4﹣1几何证明选讲】
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E、F分别为弦AB与弦AC上的点,且BCAE=DCAF,B、E、F、C四点共圆.
(1)证明:CA是△ABC外接圆的直径;
(2)若DB=BE=EA,求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二阶矩阵M有特征值λ=8及对应的一个特征向量 ![]() =[
=[ ![]() ],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
(1)求矩阵M;
(2)求矩阵M的另一个特征值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,点![]() (n∈N*)均在函数y=3x-2的图象上.
(n∈N*)均在函数y=3x-2的图象上.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如下程序框图,如果输出i=5,那么在空白矩形框中应填入的语句为( ) 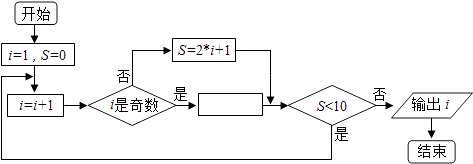
A.S=2*i﹣2
B.S=2*i﹣1
C.S=2*I
D.S=2*i+4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)平面内动点![]() 到两定点
到两定点![]() ,
,![]() 距离之比为常数
距离之比为常数![]() ,则动点
,则动点![]() 的轨迹叫做阿波罗尼斯圆.现已知定点
的轨迹叫做阿波罗尼斯圆.现已知定点![]() 、
、![]() ,圆心为
,圆心为![]() ,
,
(1)求满足上述定义的圆![]() 的方程,并指出圆心
的方程,并指出圆心![]() 的坐标和半径;
的坐标和半径;
(2)若![]() ,且经过点
,且经过点![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,当
两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com