Question

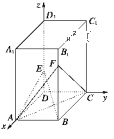
【题目】如图，在正四棱柱中，已知AB＝2， ，

E、F分别为、上的点，且.

(1)求证：BE⊥平面ACF；

(2)求点E到平面ACF的距离．

Answer 1

【答案】（1）见解析（2）

【解析】

分析：（1）以为原点，所在直线分别为轴建立空间直角坐标系，写出要用的点的坐标，要证明线与面垂直，只需证明这条直线与平面上的两条直线垂直即可；（2）为平面的一个法向量，向量在上的射影长即为到平面的距离，根据点到面的距离公式可得到结论.

详解：(1)证明：以D为原点，DA、DC、DD1所在直线分别为x、y、z轴建立如图所示空间直角坐标系，则D(0,0,0)、A(2,0,0)、B(2,2,0)、C(0,2,0)、D1(0,0,5)、E(0,0,1)、F(2,2,4)．

∴＝(－2,2,0)、＝(0,2,4)、＝(－2，－2,1)、＝(－2，0,1)．

∵·＝0，·＝0，

∴BE⊥AC，BE⊥AF，且AC∩AF＝A.

∴BE⊥平面ACF.

(2)由(1)知，为平面ACF的一个法向量，

∴点E到平面ACF的距离d＝＝.

故点E到平面ACF的距离为.