练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    f(x)＝lg，比较f(x＋1)与f(x)＋f(1)的大小．

    答案：
    解析：

    　　f(x＋1)－[f(x)＋f(1)]

    　　　　2分

    　　真数作差得：(10X－1－10－X－1)　　6分

    　　∴①x＝0时，f(x＋1)＝[f(x)＋f(1)]　　8分

    　　②x＞0时，f(x＋1)＞[f(x)＋f(1)]　　10分

    　　③x＜0时，f(x＋1)＜[f(x)＋f(1)]　　12分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    已知f(x)＝lg，A＝f(x＋1)，B＝f(x)＋f(1)，比较A与B的大小．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    已知f(x)＝lg，A＝f(x＋1)，B＝f(x)＋f(1)，比较A与B的大小．

    查看答案和解析>>

    科目：高中数学 来源：2002年全国各省市高考模拟试题汇编 题型：044

    已知f(x)＝＋(m＋1)x＋lg|m＋2|，(m≠－2，m∈R)．

    (Ⅰ)若f(x)能表示为一个奇函数g(x)和一个偶函数h(x)的和，求g(x)和h(x)的解析表达式；

    (Ⅱ)若f(x)和g(x)在区间[lg|m＋2|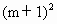，]上都是减函数，求m的取值范围；

    (Ⅲ)在(Ⅱ)的条件下，比较f(1)和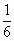的大小．

    查看答案和解析>>

    科目：高中数学 来源：河北省正定中学2010届高三上学期期中考试数学理科试题 题型：044

    已知函数f(x)＝x2＋(a＋1)x＋lg|a＋2|(a∈R，且a≠－2)．

    (1)若f(x)能表示成一个奇函数g(x)和一个偶函数h(x)的和，求g(x)和h(x)的解析式；

    (2)命题P：函数f(x)在区间[(a＋1)2，＋∞)上是增函数；命题Q：函数g(x)是减函数．如果命题P、Q有且仅有一个是真命题，求a的取值范围；

    (3)在(2)的条件下，比较f(2)与3－lg2的大小．

    查看答案和解析>>

    同步练习册答案