
【题目】已知函数f(x)=4tanxsin( ![]() ﹣x)cos(x﹣
﹣x)cos(x﹣ ![]() )﹣
)﹣ ![]() .
.
(1)求f(x)的定义域与最小正周期;
(2)讨论f(x)在区间[﹣ ![]() ,
, ![]() ]上的单调性.
]上的单调性.
【答案】
(1)解:∵f(x)=4tanxsin( ![]() ﹣x)cos(x﹣
﹣x)cos(x﹣ ![]() )﹣
)﹣ ![]() .
.
∴x≠kπ+ ![]() ,即函数的定义域为{x|x≠kπ+
,即函数的定义域为{x|x≠kπ+ ![]() ,k∈Z},
,k∈Z},
则f(x)=4tanxcosx( ![]() cosx+
cosx+ ![]() sinx)﹣
sinx)﹣ ![]()
=4sinx( ![]() cosx+
cosx+ ![]() sinx)﹣
sinx)﹣ ![]()
=2sinxcosx+2 ![]() sin2x﹣
sin2x﹣ ![]()
=sin2x+ ![]() (1﹣cos2x)﹣
(1﹣cos2x)﹣ ![]()
=sin2x﹣ ![]() cos2x
cos2x
=2sin(2x﹣ ![]() ),
),
则函数的周期T= ![]()
(2)解:由2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,即函数的增区间为[kπ﹣
,k∈Z,即函数的增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z,
],k∈Z,
当k=0时,增区间为[﹣ ![]() ,
, ![]() ],k∈Z,
],k∈Z,
∵x∈[﹣ ![]() ,
, ![]() ],∴此时x∈[﹣
],∴此时x∈[﹣ ![]() ,
, ![]() ],
],
由2kπ+ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
得kπ+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,即函数的减区间为[kπ+
,k∈Z,即函数的减区间为[kπ+ ![]() ,kπ+
,kπ+ ![]() ],k∈Z,
],k∈Z,
当k=﹣1时,减区间为[﹣ ![]() ,﹣
,﹣ ![]() ],k∈Z,
],k∈Z,
∵x∈[﹣ ![]() ,
, ![]() ],∴此时x∈[﹣
],∴此时x∈[﹣ ![]() ,﹣
,﹣ ![]() ],
],
即在区间[﹣ ![]() ,
, ![]() ]上,函数的减区间为∈[﹣
]上,函数的减区间为∈[﹣ ![]() ,﹣
,﹣ ![]() ],增区间为[﹣
],增区间为[﹣ ![]() ,
, ![]() ].
].
【解析】(1)利用三角函数的诱导公式以及两角和差的余弦公式,结合三角函数的辅助角公式进行化简求解即可.(2)利用三角函数的单调性进行求解即可.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】点M,N分别是正方体ABCD﹣A1B1C1D1的棱BB1和B1C1的中点,则MN和CD1所成角的大小为( )
A.30°
B.60°
C.90°
D.120°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体OABC﹣O′A′B′C′中,E,F分别是棱AB,BC上的动点. 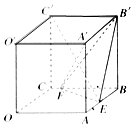
(1)当AE=BF时,求证A′F⊥C′E;
(2)若E,F分别为AB,BC的中点,求直线O′B与平面B′EF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面是正方形,侧面PAD⊥底面ABCD,且PA=PD= ![]() AD,若E、F分别为PC、BD的中点.
AD,若E、F分别为PC、BD的中点.
(Ⅰ) 求证:EF∥平面PAD;
(Ⅱ) 求证:EF⊥平面PDC.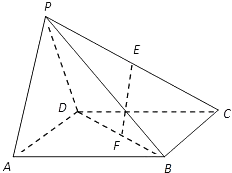
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(Ⅰ)求第一次检测出的是次品且第二次检测出的是正品的概率;
(Ⅱ)已知每检测一件产品需要费用100元,设![]() 表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求
表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题: ①函数 ![]() 的一条对称轴是x=
的一条对称轴是x= ![]() ;
;
②函数y=tanx的图象关于点( ![]() ,0)对称;
,0)对称;
③正弦函数在第一象限为增函数;
④若 ![]() ,则x1﹣x2=kπ,其中k∈Z;
,则x1﹣x2=kπ,其中k∈Z;
⑤函数f(x)=sinx+2|sinx|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围为(1,3).
以上五个命题中正确的有(填写所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O的方程为x2+y2=4,P是圆O上的一个动点,若线段OP的垂直平分线总是被平面区域|x|+|y|≥a覆盖,则实数a的取值范围是( )
A.0≤a≤2
B.![]()
C.0≤a≤1
D.a≤1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com