
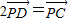 ,且有
,且有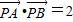 ,
,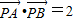 ,求得P(x',y')满足的方程:(x')2+(y')2=4…(*).再由
,求得P(x',y')满足的方程:(x')2+(y')2=4…(*).再由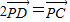 ,可得x'=2x-1,y'=2y,代入(*)式得(2x-1)2+(2y)2=4,化简即得点D的轨迹方程.
,可得x'=2x-1,y'=2y,代入(*)式得(2x-1)2+(2y)2=4,化简即得点D的轨迹方程. +cosα,sinα),用点到直线的距离公式求得D到AB距离的最大值为1+
+cosα,sinα),用点到直线的距离公式求得D到AB距离的最大值为1+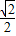 ,由此即可得到△ABD面积的最大值;
,由此即可得到△ABD面积的最大值; )2+y2=1在x2+y2=2内的劣弧上,求出界点处的切线斜率,再观察直线l的斜率的变化,可得斜率k的取值范围.
)2+y2=1在x2+y2=2内的劣弧上,求出界点处的切线斜率,再观察直线l的斜率的变化,可得斜率k的取值范围.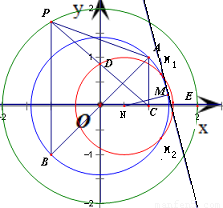 解:(1)设P(x',y'),得
解:(1)设P(x',y'),得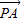 =(1-x',1-y'),
=(1-x',1-y'),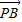 =(-1-x',-1-y'),
=(-1-x',-1-y'),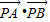 =(1-x')(-1-x')+(1-y')(-1-y')=(x')2+(y')2-2
=(1-x')(-1-x')+(1-y')(-1-y')=(x')2+(y')2-2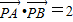 ,
,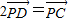 得D为PC的中点
得D为PC的中点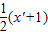 ,y'=
,y'=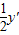 .
. )2+y2=1
)2+y2=1 +cosα,sinα),
+cosα,sinα),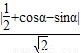 =
=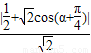
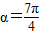 时,d的最大值为1+
时,d的最大值为1+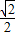 ,
, ×AB×(1+
×AB×(1+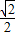 )=1+
)=1+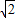 ;
; ,
,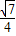 )和M2(
)和M2( ,-
,-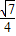 )
) )2+y2=1在x2+y2=2内的劣弧上
)2+y2=1在x2+y2=2内的劣弧上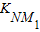 =
=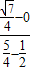 =
=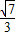 ,得此时切线l的斜率k1=
,得此时切线l的斜率k1=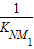 =-
=-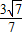
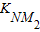 =
= =-
=-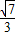 ,得此时切线l的斜率k2=
,得此时切线l的斜率k2= =
=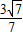
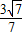 )∪(
)∪(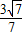 ,+∞)
,+∞)

科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com