
.设函数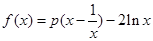 ,
, (
(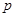 是实数,
是实数,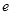 为自然对数的底数)
为自然对数的底数)
(1)若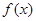 在其定义域内为单调函数,求
在其定义域内为单调函数,求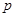 的取值范围;
的取值范围;
(2)若在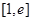 上至少存在一点
上至少存在一点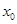 0,使得
0,使得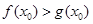 成立,求
成立,求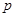 的取值范围。
的取值范围。
(1) p≥1或p≤0
(2)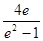 ,+∞)
,+∞)
【解析】
(1)∵f’(x)=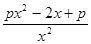 ,要使f(x)为单调增函数,须f’(x)≥0恒成立,即px2-2x+p≥0恒成立,即p≥
,要使f(x)为单调增函数,须f’(x)≥0恒成立,即px2-2x+p≥0恒成立,即p≥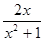 =
=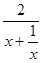 恒成立,又
恒成立,又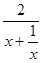 ≤1,
≤1,
所以当p≥1时,f(x)在(0,+∞)为单调增函数。
要使f(x)为单调减函数,须f’(x) ≤0恒成立,
即px2-2x+0≤0恒成立,即p≤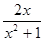 =
=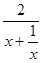 恒成立,又
恒成立,又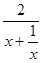 >0,
>0,
所以当p≤0时,f(x)在(0,+ ∞)为单调减函数。
综上所述,f(x)在(0,+∞)为单调函数,p的取值范围为p≥1或p≤0…(6分)
(2)因g(x)=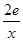 在[1,e]上为减函数,所以g(x)∈[2,2e]
在[1,e]上为减函数,所以g(x)∈[2,2e]
①当p≤0时,由(1)知f(x)在[1,e]上递减 f(x)max=f(1)=0<2,不合题意
f(x)max=f(1)=0<2,不合题意
②当p≥1时,由(1)知f(x)在[1,e]上递增,f(1) <2,又g(x)在[1,e]上为减函数,故只需f(x)max>g(x)min,x∈[1,e],
即:f(e)=p(e- )-2lne>2
)-2lne>2 p>
p>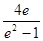 .
.
③当0<p<1时,因x- ≥0,x∈[1,e]
≥0,x∈[1,e]
所以f(x)=p(x- )-2lnx≤(x-
)-2lnx≤(x- )-2lnx≤e-
)-2lnx≤e- -2lne<2不合题意
-2lne<2不合题意
综上,p的取值范围为(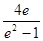 ,+∞)……………………………………(12分)
,+∞)……………………………………(12分)


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源:中学教材全解 高中数学 必修1(人教A版) 人教A版 题型:047
设函数f(x)是实数集R上的增函数,令F(x)=f(x)-f(2-x).
(1)求证:F(x)在R上是增函数;
(2)若F(x1)+F(x2)>0,求证:x1+x2>2.
查看答案和解析>>
科目:高中数学 来源:四川省平武中学2011届高三一诊模拟演练文科数学试题 题型:013
设函数f(x)是实数集R上以5为周期的可导偶函数,则曲线y=f(x)在x=2010处的切线的斜率为
-![]()
0
![]()
5
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
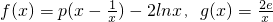 (p是实数,e是自然对数的底数)
(p是实数,e是自然对数的底数)查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省安庆市潜山中学高三(上)第三次月考数学试卷(理科)(解析版) 题型:解答题
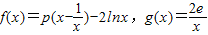 (p是实数,e是自然对数的底数)
(p是实数,e是自然对数的底数)查看答案和解析>>
科目:高中数学 来源:2011年浙江省杭州市萧山区高考数学模拟试卷13(理科)(解析版) 题型:解答题
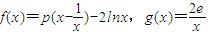 (p是实数,e是自然对数的底数)
(p是实数,e是自然对数的底数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com