
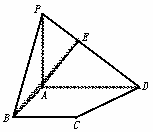
图10-24
(Ⅰ)若AE⊥PD,E为垂足,求证:BE⊥PD;
(Ⅱ)求异面直线AE与CD所成角的大小(用反三角函数表示).
(Ⅰ)方法一:如图10-57(1)
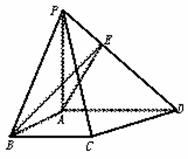
图10-57(1)
∵PA⊥平面ABCD,
∴PA⊥AB,再由AB⊥AD,得AB⊥平面PAD,
∴AB⊥PD.
又∵AE⊥PD,∴PD⊥平面ABE,故BE⊥PD.
方法二:由题设AB⊥AD,AB⊥AP,∴AB⊥平面PAD,
故由AB⊥平面PAD,AE⊥PD,得BE⊥PD.
(Ⅱ)方法一:如图10-57(2),以A为原点,AB、AD、AP所在直线为坐标轴,建立空间直角坐标系,
则点C、D的坐标分别为(a,a,0),(0,2a,0).
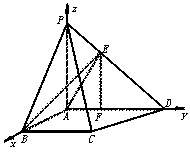
图10-57(2)
∵PA⊥平面ABCD,得∠PDA是PD与底面ABCD所成的角.
∴∠PDA=30°,
于是在Rt△AED中,由AD=2a,得AE=a,
过E作EF⊥AD,垂足为F,
在Rt△AFE中,由AE=a,∠EAF=60°,
得AF=![]() a,EF=
a,EF=![]() a,
a,
∴E(0,![]() a,
a,![]() a).
a).
于是![]() =
=![]() ,
,![]() ={-a,a,0}.
={-a,a,0}.
设![]() 与
与![]() 的夹角为θ,则由
的夹角为θ,则由
cosθ=![]() =
=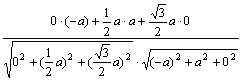 =
=![]() ,
,
得θ=arccos![]() ,
,
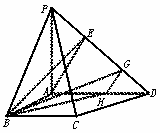
图10-57(3)
即AE与CD所成角的大小为arccos![]() .
.
方法二:如图10-57(3),设G、H分别为ED、AD的中点,连结BH、HG、GB,
易知DH平行且等于CB,
∴BH∥CD,
∵G、H分别为ED、AD的中点,
∴HG∥AE,
则∠BHG或它的补角就是异面直线AE、CD所成的角.
而HG=![]() ,AE=
,AE=![]() a,BH=
a,BH=![]() =
=![]() a,
a,
BG2=BE2+EG2=AB2+AE2+EG2=![]() a2,
a2,
在△BHG中,由余弦定理可得cos∠BHG=![]() =-
=-![]() .
.
∠BHG=π-arccos![]() ,
,
所以异面直线AE、CD所成角的大小为arccos![]() .
.


科目:高中数学 来源:2011-2012学年辽宁省葫芦岛市五校协作体高三8月模拟考试文科数学 题型:解答题
四、选做题(本小题满分10分。请考生22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分)
22.选修4-1:几何证明选讲
如图,已知点C在圆O直径BE的延长线上,CA切
圆O于A点,DC是∠ACB的平分线并交AE于点F、交
AB于D点,则∠ADF=?
|
查看答案和解析>>
科目:高中数学 来源: 题型:
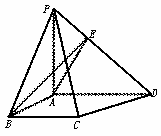
图10-24
(Ⅰ)若AE⊥PD,E为垂足,求证:BE⊥PD;
(Ⅱ)求异面直线AE与CD所成角的大小(用反三角函数表示).
查看答案和解析>>
科目:高中数学 来源:2012届辽宁省葫芦岛市五校协作体高三8月模拟考试文科数学 题型:解答题
四、选做题(本小题满分10分。请考生22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分)
22.选修4-1:几何证明选讲
如图,已知点C在圆O直径BE的延长线上,CA切
圆O于A点,DC是∠ACB的平分线并交AE于点F、交
AB于D点,则∠ADF=?
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com