
如图,在四棱柱 中,底面ABCD和侧面
中,底面ABCD和侧面 都是矩形,E是CD的中点,
都是矩形,E是CD的中点, ,
, .
.
(1)求证: ;
;
(2)若平面 与平面
与平面 所成的锐二面角的大小为
所成的锐二面角的大小为 ,求线段
,求线段 的长度.
的长度.
(1)证明过程详见解析;(2) .
.
解析试题分析:本题主要考查线线垂直、线面垂直、面面垂直、二面角等基础知识,考查学生的空间想象能力、逻辑推理能力、计算能力.第一问,由已知得 ,
, ,所以利用线面平行的判定得
,所以利用线面平行的判定得 平面
平面 ,再利用线面垂直的性质,得
,再利用线面垂直的性质,得 ;第二问,可以利用传统几何法求二面角的平面角,也可以利用向量法求平面
;第二问,可以利用传统几何法求二面角的平面角,也可以利用向量法求平面 和平面
和平面 的法向量,利用夹角公式列出方程,通过解方程,求出线段
的法向量,利用夹角公式列出方程,通过解方程,求出线段 的长度..
的长度..
(1)证明:∵底面 和侧面
和侧面 是矩形,
是矩形,
∴ ,
,
又∵
∴ 平面
平面 3分
3分
∵ 平面
平面 ∴
∴ . 6分
. 6分
(2)
解法1:延长 ,
, 交于
交于 ,连结
,连结 ,
,
则平面
 平面
平面

底面 是矩形,
是矩形, 是
是 的中点,
的中点, ,∴连结
,∴连结 ,则
,则
又由(1)可知
又∵ ,
,
∴
 底面
底面 ,∴
,∴ ∴
∴ 平面
平面 9
9
过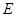 作
作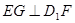 于
于 ,连结
,连结 ,则
,则 是平面
是平面 与平面
与平面 即平面
即平面 与平面
与平面 所成锐二面角的平面角,所以
所成锐二面角的平面角,所以
又 ,∴
,∴
又易得 ,
, ,从而由
,从而由 ,求得
,求得 . 12分
. 12分
解法2:由(1)可知
又∵ ,
, ∴
∴
 底面
底面 7分
7分
设 为
为 的中点,以
的中点,以

科目:高中数学 来源: 题型:解答题
如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°.
(1)证明:平面PAB与平面PCD的交线平行于底面;
(2)求cos∠COD.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知四棱锥 ,底面
,底面 为矩形,侧棱
为矩形,侧棱 ,其中
,其中 ,
, 为侧棱
为侧棱 上的两个三等分点,如下图所示.
上的两个三等分点,如下图所示.
(1)求证: ;
;
(2)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)求二面角 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2011•山东)如图,在四棱台ABCD﹣A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.
(1)证明:AA1⊥BD;
(2)证明:CC1∥平面A1BD.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥P-ABCD中,侧面PAD 底面ABCD,侧棱
底面ABCD,侧棱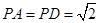 ,底面ABCD为直角梯形,其中BC//AD,AB
,底面ABCD为直角梯形,其中BC//AD,AB AD,AD=2,AB=BC=l,E为AD中点.
AD,AD=2,AB=BC=l,E为AD中点.
(1)求证:PE 平面ABCD:
平面ABCD:
(2)求异面直线PB与CD所成角的余弦值:
(3)求平面PAB与平面PCD所成的二面角.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形. 
(1)求证DM∥平面APC;
(2)求证平面ABC⊥平面APC;
(3)若BC=PC=4,求二面角P-AB-C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四棱锥 中,底面
中,底面 是平行四边形,
是平行四边形, ,
, 平面
平面 ,
, ,
, ,
, 是
是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)若以 为坐标原点,射线
为坐标原点,射线 、
、 、
、 分别是
分别是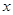 轴、
轴、 轴、
轴、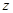 轴的正半轴,建立空间直角坐标系,已经计算得
轴的正半轴,建立空间直角坐标系,已经计算得 是平面
是平面 的法向量,求平面
的法向量,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com