
【题目】设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和.已知S3=7,且a1+3,3a2 , a3+4构成等差数列.
(1)求数列{an}的通项公式.
(2)令bn=lna3n+1 , n=1,2,…,求数列{bn}的前n项和Tn .
【答案】
(1)解:由已知得 
解得a2=2.
设数列{an}的公比为q,由a2=2,
可得 ![]() .
.
又S3=7,可知 ![]() ,
,
即2q2﹣5q+2=0,
解得 ![]()
由题意得q>1,
∴q=2,
∴a1=1.故数列{an}的通项为an=2n﹣1
(2)解:由于bn=lna3n+1,n=1,2,
由(1)得a3n+1=23n,
∴bn=ln23n=3nln2,又bn+1﹣bn=3ln2,
∴{bn}是等差数列.
∴Tn=b1+b2++bn
= ![]()
= ![]()
= ![]() .
.
故 ![]()
【解析】(1)由{an}是公比大于1的等比数列,S3=7,且a1+3,3a2 , a3+4构成等差数列,我们不难构造方程组,解方程组即可求出相关基本量,进而给出数列{an}的通项公式.(2)由bn=lna3n+1 , n=1,2,…,我们易给出数列{bn}的通项公式,分析后可得:数列{bn}是一个等差数列,代入等差数列前n项和公式即可求出Tn
【考点精析】解答此题的关键在于理解等比数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() ,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系
,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系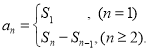 .
.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义域为
定义域为![]() ,若对于任意的
,若对于任意的![]() ,都有
,都有![]() ,且
,且![]() 时,有
时,有![]() .
.
(1)判断并证明函数![]() 的奇偶性;
的奇偶性;
(2)判断并证明函数![]() 的单调性;
的单调性;
(3)设![]() ,若
,若![]() ,对所有
,对所有![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,函数g(x)=b﹣f(2﹣x),其中b∈R,若函数y=f(x)﹣g(x)恰有4个零点,则b的取值范围是( )
,函数g(x)=b﹣f(2﹣x),其中b∈R,若函数y=f(x)﹣g(x)恰有4个零点,则b的取值范围是( )
A.( ![]() ,+∞)
,+∞)
B.(﹣∞, ![]() )
)
C.(0, ![]() )
)
D.( ![]() ,2)
,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种设备的单价为![]() 元,设备维修和消耗费用第一年为
元,设备维修和消耗费用第一年为![]() 元,以后每年增加
元,以后每年增加![]() 元(
元(![]() 是常数).用
是常数).用![]() 表示设备使用的年数,记设备年平均费用为
表示设备使用的年数,记设备年平均费用为![]() ,即
,即![]() (设备单价
(设备单价![]() 设备维修和消耗费用)
设备维修和消耗费用)![]() 设备使用的年数.
设备使用的年数.
(Ⅰ)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)当![]() ,
, ![]() 时,求这种设备的最佳更新年限.
时,求这种设备的最佳更新年限.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]()
![]() .
.
(1)请写出fn(x)的表达式(不需证明);
(2)设fn(x)的极小值点为Pn(xn , yn),求yn;
(3)设 ![]() ,gn(x)的最大值为a,fn(x)的最小值为b,求b﹣a的最小值.
,gn(x)的最大值为a,fn(x)的最小值为b,求b﹣a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x与相应的生产能耗y的几组对照数据
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() .(其中
.(其中 ,
, ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax﹣lnx,a∈R.
(1)若函数f(x)在[1,2]上是减函数,求实数a的取值范围;
(2)令g(x)=f(x)﹣x2 , 是否存在实数a,当x∈(0,e](e是自然常数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com