
【题目】已知抛物线C:y2=2px过点P(1,1).过点(0,![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.
(Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A为线段BM的中点.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某学校高一 、高二 、高三三个年级共有 ![]() 名教师,为调查他们的备课时间情况,通过分层
名教师,为调查他们的备课时间情况,通过分层
抽样获得了![]() 名教师一周的备课时间 ,数据如下表(单位 :小时):
名教师一周的备课时间 ,数据如下表(单位 :小时):
高一年级 |
|
|
|
|
| |||
高二年级 |
|
|
|
|
|
|
| |
高三年级 |
|
|
|
|
|
|
|
|
(1)试估计该校高三年级的教师人数 ;
(2)从高一年级和高二年级抽出的教师中,各随机选取一人,高一年级选出的人记为甲 ,高二年级选出的人记为乙 ,求该周甲的备课时间不比乙的备课时间长的概率 ;
(3)再从高一、高二、高三三个年级中各随机抽取一名教师,他们该周的备课时间分别是![]() (单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为
(单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为![]() ,表格中的数据平均数记为
,表格中的数据平均数记为![]() ,试判断
,试判断![]() 与
与![]() 的大小. (结论不要求证明)
的大小. (结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络营销部门为了统计某市网友2015年11月11日在某网店的网购情况,随机抽查了该市100名网友的网购金额情况,得到如下频率分布直方图.
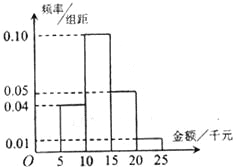
(1)估计直方图中网购金额的中位数;
(2)若规定网购金额超过15千元的顾客定义为“网购达人”,网购金额不超过15千元的顾客定义为“非网购达人”;若以该网店的频率估计全市“非网购达人”和“网购达人”的概率,从全市任意选取3人,则3人中“非网购达人”与“网购达人”的人数之差的绝对值为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x+1)= ![]() ,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
A.f(sinα)>f(sinβ)
B.f(cosα)>f(cosβ)
C.f(sinα)>f(cosβ)
D.f(sinα)<f(cosβ)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(ax+1)+mx是偶函数.
(1)求m;
(2)当a>1时,若函数f(x)的图像与直线l:y=﹣mx+n无公共点,求n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn . 已知a1=1, ![]() =an+1﹣
=an+1﹣ ![]() n2﹣n﹣
n2﹣n﹣ ![]() ,n∈N* .
,n∈N* .
(1)求数列{an}的通项公式;
(2)设数列{bn}满足an﹣an﹣1=bna ![]() ,求数列{bn}的n前项和Tn;
,求数列{bn}的n前项和Tn;
(3)是否存在实数λ,使得不等式λa ![]() ﹣
﹣ ![]() +a
+a ![]() +
+ ![]() ≥0恒成立,若存在,求出λ的取值范围;若不存在,请说明理由.
≥0恒成立,若存在,求出λ的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x2+ax+3.
(1)当x∈R时,f(x)≥a恒成立,求a的取值范围.
(2)当x∈[﹣2,2]时,f(x)≥a恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com