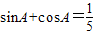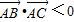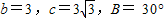练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    由下面的条件能得出△ABC为锐角三角形的是（ ）
    A．
    B．
    C．cosAcosBcos（A+B）＜0
    D．
    【答案】分析：对于A，两边平方得，可知A为钝角；对于B，，可知夹角A为钝角；对于C，cosAcosBcosC＞0，从而三余弦均为正，故正确；对于D，有两解，C为60°或120°．
    解答：解：由题意，对于A，两边平方得，∴A为钝角；
    对于B，，∴A为钝角；
    对于C，由cosAcosBcos（A+B）＜0 可得cosAcosBcosC＞0，从而可知三余弦均为正，从而三角形为锐角三角形；
    对于D，，C为60°或120°．
    故选C．
    点评：本题以判断三角形形状为载体，考查三角函数，考查正弦定理，有一定的综合性．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    由下面的条件能得出△ABC为锐角三角形的是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    由下面的条件能得出△ABC为锐角三角形的是


    1. A.
      数学公式
    2. B.
      数学公式
    3. C.
      cosAcosBcos（A+B）＜0
    4. D.
      数学公式

    查看答案和解析>>

    同步练习册答案