
(14分) 已知函数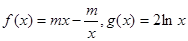 .
.
(1)当 时,求曲线
时,求曲线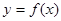 在点
在点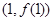 处的切线方程;
处的切线方程;
(2)当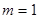 时,判断方程
时,判断方程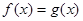 实根个数.
实根个数.
(3)若 时,不等式
时,不等式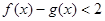 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1) ;(2)在
;(2)在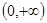 内
内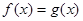 有且仅有一个实数根
有且仅有一个实数根
(3)
解析试题分析:(1)利用导数的几何意义得到导数的值,切点坐标得到结论。
(2)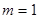 时,令
时,令 ,
,
求解导数,并判定又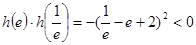 ,
,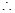
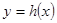 在
在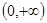 内有且仅有一个零点进而得到结论。
内有且仅有一个零点进而得到结论。
(3)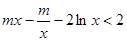 恒成立, 即
恒成立, 即 恒成立,
恒成立,
又 ,则当
,则当 时,
时,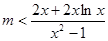 恒成立,
恒成立,
分离参数法构造新函数利用求解的最小值得到参数m的范围。
(1) 时,
时, ,
, ,切点坐标为
,切点坐标为 ,
,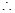 切线方程为
切线方程为
(2)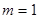 时,令
时,令 ,
, ,
, 在
在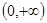 上为增函数
上为增函数
又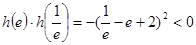 ,
,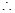
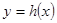 在
在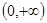 内有且仅有一个零点
内有且仅有一个零点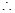 在
在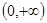 内
内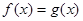 有且仅有一个实数根
有且仅有一个实数根
(或说明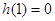 也可以)
也可以)
(3)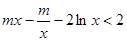 恒成立, 即
恒成立, 即 恒成立,
恒成立,
又 ,则当
,则当 时,
时,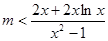 恒成立,
恒成立,
令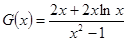 ,只需
,只需 小于
小于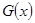 的最小值,
的最小值,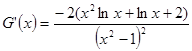 ,
,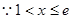 ,
, ,
,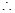 当
当 时
时 ,
,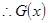 在
在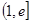 上单调递减,
上单调递减,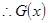 在
在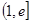 的最小值为
的最小值为 ,
,
则 的取值范围是
的取值范围是
考点:本题主要是考查导数在研究函数中的运用,求解最值和导数几何意义的综合运用。
点评:解决该试题的关键是能将不等式的恒成立问题转化为哈双女户的最值来处理,并得到参数的范围,同时要理解导数的几何意义表示的为切线的斜率。


科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函數f(x)=ln+mx2(m∈R)
(I)求函数f(x)的单调区间;
(II)若A,B是函数f(x)图象上不同的两点,且直线AB的斜率恒大于1,求实数m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分16分)
已知函数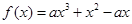 ,其中
,其中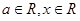 .
.
(1)当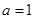 时,求函数
时,求函数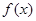 在
在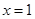 处的切线方程;
处的切线方程;
(2)若函数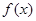 在区间(1,2)上不是单调函数,试求
在区间(1,2)上不是单调函数,试求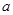 的取值范围;
的取值范围;
(3)已知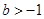 ,如果存在
,如果存在 ,使得函数
,使得函数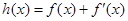
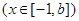 在
在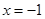 处取得最小值,试求
处取得最小值,试求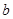 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知数列 的前
的前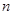 项和为
项和为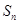 ,函数
,函数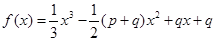 ,
,
(其中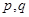 均为常数,且
均为常数,且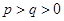 ),当
),当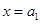 时,函数
时,函数 取得极小值.
取得极小值.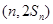
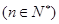 均在函数
均在函数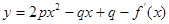 的图像上(其中
的图像上(其中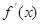 是
是 的导函数).
的导函数).
(Ⅰ)求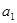 的值;
的值;
(Ⅱ)求数列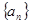 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)(注意:仙中、一中、八中的学生三问全做,其他学校的学生只做前两问)
已知函数
(Ⅰ)若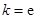 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(Ⅱ)若 ,且对于任意
,且对于任意 ,
, 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(Ⅲ)设函数 ,求证:
,求证: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com