
设关于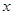 的二次函数
的二次函数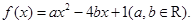
(I)设集合P={1,2, 4}和Q={-1,1,2},分别从集合P和Q中随机取一个数作为函数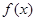 中
中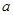 和
和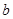 的值,求函数
的值,求函数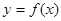 有且只有一个零点的概率;
有且只有一个零点的概率;
(II)设点(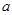 ,
,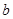 )是随机取自平面区域
)是随机取自平面区域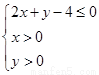 内的点,求函数
内的点,求函数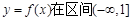 上是减函数的概率.
上是减函数的概率.
(I)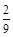
(II)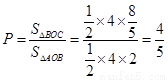
【解析】解:(I)要使函数 有且只有一个零点,当且仅当
有且只有一个零点,当且仅当 ……………………………2分
……………………………2分
分别从集合P和Q中随机取一个数作为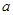 和
和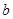 ,可以是
,可以是 共9个基本事件,其中满足
共9个基本事件,其中满足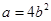 的事件有
的事件有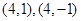 共2个,
共2个,
∴所求事件的概率为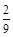 .
……………………………6分
.
……………………………6分
(II) 函数
函数 的图象的对称轴为
的图象的对称轴为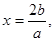
由函数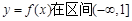 上是减函数,得
上是减函数,得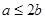 且
且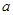 >0,....8分
>0,....8分
依条件可知试验的全部结果所构成的区域为 ,即三角形区域
,即三角形区域 .且
.且  .......................................10分
.......................................10分
构成所求事件的区域为三角形区域 (如图).
(如图).

由 ……………………………12分
……………………………12分
∴所求事件的概率为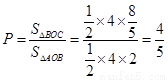 ………………… 13分
………………… 13分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2011-2012学年黑龙江省高三上学期期末考试文科数学试卷 题型:解答题
已知关于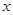 的二次函数
的二次函数 ,
,
(1)设集合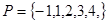 ,和
,和 分别从集合
分别从集合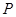 和
和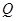 中随机取出一个数作为
中随机取出一个数作为 和
和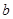 ,求函数
,求函数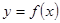 在区间
在区间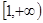 上是增函数的概率;
上是增函数的概率;
(2)设 是区域
是区域
 的随机点,求函数
的随机点,求函数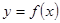 在区间
在区间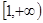 上是增函数的概率。
上是增函数的概率。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省高三上学期期末考试文科数学卷 题型:解答题
设关于 的二次函数
的二次函数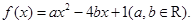
(I)设集合P={1,2, 4}和Q={-1,1,2},分别从集合P和Q中随机取一个数作为函数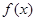 中
中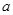 和
和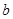 的值,求函数
的值,求函数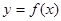 有且只有一个零点的概率;
有且只有一个零点的概率;
(II)设点(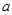 ,
,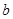 )是随机取自平面区域
)是随机取自平面区域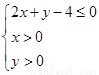 内的点,
内的点,
求函数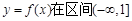 上是减函数的概率.
上是减函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)
设关于![]() 的二次函数
的二次函数![]()
(I)设集合P={1,2, 4}和Q={-1,1,2},分别从集合P和Q中随机取一个数作为函数![]() 中
中![]() 和
和![]() 的值,求函数
的值,求函数![]() 有且只有一个零点的概率;
有且只有一个零点的概率;
(II)设点(![]() ,
,![]() )是随机取自平面区域
)是随机取自平面区域 内的点,求函数
内的点,求函数![]() 上是减函数的概率.
上是减函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知关于![]() 的二次函数
的二次函数![]() 。
。
(1)设集合![]() 和
和![]() ,分别从集合P和Q中随机取一个数作为
,分别从集合P和Q中随机取一个数作为![]() ,求函数
,求函数![]() 在区间
在区间![]() 上是增函数的概率;
上是增函数的概率;
(2)设点![]() 是区域
是区域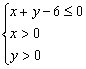 内的随机点,求函数
内的随机点,求函数![]() 在区间
在区间![]() 上是增函数的概率。
上是增函数的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com