
在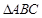 中,
中, 的对边分别为
的对边分别为 且
且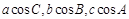 成等差数列.
成等差数列.
(1)求B的值;
(2)求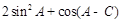 的范围.
的范围.
(1) ;(2)
;(2)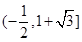
【解析】
试题分析:(1)对于三角形问题中的边角混合的式子,可以利用正弦定理和余弦定理边角转化,或边化角转化为三角函数问题,或角化边转化为代数问题来处理,该题由等差中项列式 ,再利用正弦定理边化角为,
,再利用正弦定理边化角为,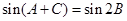 ,又根据三角形内角的关系
,又根据三角形内角的关系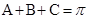 ,得
,得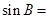
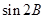 ,进而求
,进而求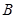 ;(2)由(1)得
;(2)由(1)得 ,可得
,可得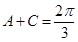 ,代入所求式中,化为自变量为
,代入所求式中,化为自变量为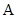 的函数解析式,再化为
的函数解析式,再化为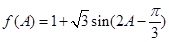 ,然后根据
,然后根据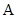 的范围,确定
的范围,确定 的范围,进而结合
的范围,进而结合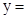
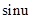 的图象确定
的图象确定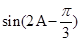 的范围,进而求
的范围,进而求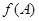 的范围.
的范围.
试题解析:(1)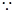
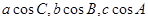 成等差数列,∴
成等差数列,∴ ,由正弦定理得,
,由正弦定理得,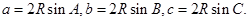 ,代入得,
,代入得,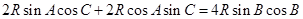 ,即:
,即: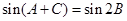 ,
, ,又在
,又在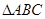 中,
中,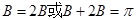 ,∵
,∵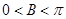 ,∴
,∴ ;
;
(2)∵ ,∴
,∴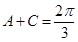 ,∴
,∴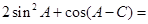
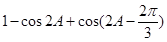 =
=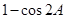
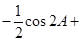
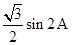 =
=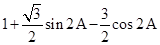 =
=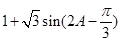 ,∵
,∵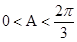 ,∴
,∴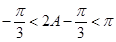 ,∴
,∴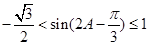 ,∴
,∴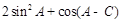 的取值范围是
的取值范围是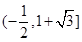 .
.
考点:1、等差中项;2、正弦定理;3、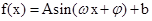 型函数的值域.
型函数的值域.


科目:高中数学 来源:2014届安徽省高三第一次月考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)在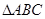 中,角
中,角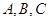 的对边分别为
的对边分别为 且
且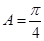 ,bsin(
,bsin(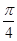 +C)-c sin(
+C)-c sin(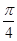 +B)=a ,
+B)=a ,
(1)求证:
(2)若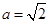 ,求
,求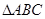 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2014届广东深圳第二高级中学高三上学期第一次月考文科数学试卷(解析版) 题型:解答题
在 中,角
中,角 的对边分别为
的对边分别为 ,且满足
,且满足
(1)求证: ;
;
(2)若 的面积
的面积 ,
, ,
,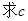 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三上学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分14分)在 中,
中,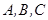 的对边分别为
的对边分别为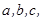 且
且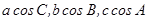 成等差数列.(1)求
成等差数列.(1)求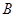 的值;(2)求
的值;(2)求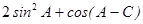 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com