
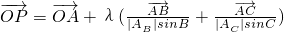 ,λ∈(0,+∞),则点P的轨迹一定经过△ABC的
,λ∈(0,+∞),则点P的轨迹一定经过△ABC的 sinB=
sinB=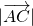 sinC=AD,由此对已知条件变形即可得出结论;
sinC=AD,由此对已知条件变形即可得出结论;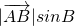 =
=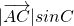 提取出来,转化成λt(
提取出来,转化成λt(  +
+ ),而λt(
),而λt(  +
+ )表示与
)表示与  共线的向量,点D是BC的中点,故P的轨迹一定通过三角形的重心.
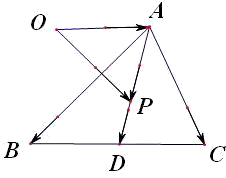
共线的向量,点D是BC的中点,故P的轨迹一定通过三角形的重心. 解:法一:作出如图的图形AD⊥BC,由于
解:法一:作出如图的图形AD⊥BC,由于  sinB=
sinB=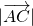 sinC=AD,
sinC=AD, =
=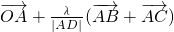
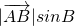 =
=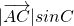 设它们等于
设它们等于 
 ∴
∴ =
= +λt(
+λt(  +
+ )
) +
+ =2
=2 
 +
+ )表示与
)表示与  共线的向量
共线的向量 


科目:高中数学 来源: 题型:
| AD |
| BC |
| AH |
| HD |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com