
【题目】如图,三棱柱ABC-![]() 中,
中,![]() ⊥平面ABC,AC⊥AB,AB=AC=2,C
⊥平面ABC,AC⊥AB,AB=AC=2,C![]() =4,D为BC的中点
=4,D为BC的中点

(I)求证:AC⊥平面AB![]() ;
;
(II)求证:![]() C∥平面AD
C∥平面AD![]() ;
;
(III)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
【答案】(Ⅰ)见解析(II)见解析(III)![]()
【解析】
(I)C![]() ⊥平面ABC,得A
⊥平面ABC,得A![]() ⊥平面ABC,从而A
⊥平面ABC,从而A![]() ⊥AC,再结合已知可证得线面垂直;
⊥AC,再结合已知可证得线面垂直;
(II)连接![]() ,与A
,与A![]() 相交于点O,连接DO,可证DO∥
相交于点O,连接DO,可证DO∥![]() ,从而证得线面平行;
,从而证得线面平行;
(III)以![]() 为
为![]() 轴建立空间直角坐标系,写出各点坐标,求出两平面
轴建立空间直角坐标系,写出各点坐标,求出两平面![]() 和平面
和平面![]() 的法向量,由法向量的夹角余弦值求得二面角的余弦值.
的法向量,由法向量的夹角余弦值求得二面角的余弦值.
(I)∵C![]() ⊥平面ABC,A
⊥平面ABC,A![]() ∥C
∥C![]()
∴A![]() ⊥平面ABC,
⊥平面ABC,
∴A![]() ⊥AC
⊥AC
又AC⊥AB,AB∩A![]() =A
=A
∴AC⊥平面AB![]() ·
·
(II)连接![]() ,与A
,与A![]() 相交于点O,连接DO
相交于点O,连接DO
∵D是BC中点,O是![]() 中点,
中点,
则DO∥![]() ,
,
![]() 平面AD
平面AD![]() ,DO
,DO![]() 平面AD
平面AD![]()
∴![]() 平面AD
平面AD![]()
(III)由(I)知,AC⊥平面AB![]() ,A
,A![]() ⊥AB
⊥AB
如图建立空间直角坐标系A-xyz·
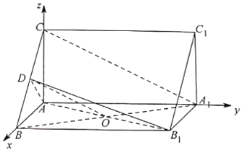
则A(0,0,0),B(2,0,0),![]() (2,4,0),D(1,0,1),
(2,4,0),D(1,0,1),![]() =(1,0,1),
=(1,0,1),![]() =(2,4,0)
=(2,4,0)
设平面AD![]() 的法向量为
的法向量为![]() =(x,y,z),则
=(x,y,z),则
![]() ,即
,即![]()
取y=1,得![]() =(-2,1,2)
=(-2,1,2)
平面AC![]() 的法向量为
的法向量为![]() =(2,0,0)
=(2,0,0)
Cos<![]() ,
,![]() >=
>=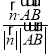 =-
=-![]() ·
·
则平面AD![]() 与平面AC
与平面AC![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了![]() 人进行分析,得到如下列联表(单位:人).
人进行分析,得到如下列联表(单位:人).
经常使用 | 偶尔使用或不使用 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)根据以上数据,能否在犯错误的概率不超过![]() 的前提下认为
的前提下认为![]() 市使用共享单车的情况与年龄有关;
市使用共享单车的情况与年龄有关;
(2)(i)现从所选取的![]() 岁以上的网友中,采用分层抽样的方法选取
岁以上的网友中,采用分层抽样的方法选取![]() 人,再从这
人,再从这![]() 人中随机选出
人中随机选出![]() 人赠送优惠券,求选出的
人赠送优惠券,求选出的![]() 人中至少有
人中至少有![]() 人经常使用共享单车的概率;
人经常使用共享单车的概率;
(ii)将频率视为概率,从![]() 市所有参与调查的网友中随机选取
市所有参与调查的网友中随机选取![]() 人赠送礼品,记其中经常使用共享单车的人数为
人赠送礼品,记其中经常使用共享单车的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式: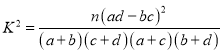 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人在塔的正东方向沿着南偏西60°的方向前进40 m以后,望见塔在东北方向上,若沿途测得塔的最大仰角为30°,则塔高为________________m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意![]() ,
,![]() ,
,![]() ,给出下列命题:
,给出下列命题:
①“![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
②“![]() 是无理数”是“
是无理数”是“![]() 是无理数”的充要条件;
是无理数”的充要条件;
③“![]() ”是“
”是“![]() ”的必要条件,
”的必要条件,
④“![]() ”是“
”是“![]() ”的充分条件.
”的充分条件.
其中真命题的个数为().
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,
的焦点,![]() 为抛物线
为抛物线![]() 上三点,且点
上三点,且点![]() 在第一象限,直线
在第一象限,直线![]() 经过点
经过点![]() 与抛物线
与抛物线![]() 在点
在点![]() 处的切线平行,点
处的切线平行,点![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() 与
与![]() 轴平行;
轴平行;
(2)求![]() 面积
面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆M:![]() =1(a>b>c)的一个顶点坐标为(0,1),焦距为2
=1(a>b>c)的一个顶点坐标为(0,1),焦距为2![]() .若直线y=x+m与椭圆M有两个不同的交点A,B
.若直线y=x+m与椭圆M有两个不同的交点A,B
(I)求椭圆M的方程;
(II)将![]() 表示为m的函数,并求△OAB面积的最大值(O为坐标原点)
表示为m的函数,并求△OAB面积的最大值(O为坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省数学学业水平考试成绩共分为![]() 、
、![]() 、
、![]() 、
、![]() 四个等级,在学业水平考试成绩分布后,从该省某地区考生中随机抽取
四个等级,在学业水平考试成绩分布后,从该省某地区考生中随机抽取![]() 名考生,统计他们的数学成绩,部分数据如下:
名考生,统计他们的数学成绩,部分数据如下:
等级 |
|
|
|
|
频数 |
|
| ||
频率 |
|
(1)补充完成上述表格的数据;
(2)现按上述四个等级,用分层抽样方法从这![]() 名考生中抽取
名考生中抽取![]() 名.在这
名.在这![]() 名考生中,从成绩为
名考生中,从成绩为![]() 等和
等和![]() 等的所有考生中随机抽取
等的所有考生中随机抽取![]() 名,求至少有
名,求至少有![]() 名成绩为
名成绩为![]() 等的概率.
等的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com